题目内容
17.观察下列各式,并用所得出的规律解决问题:(1)$\sqrt{2}$=1.414,$\sqrt{200}$=14.14,$\sqrt{20000}$=141.4…
$\sqrt{0.03}$=0.1732,$\sqrt{3}$=1.732,$\sqrt{300}$=17.32…
由此可见,被开方数的小数点每向右移动两位,其算术平方根的小数点向右移动一位;
(2)已知$\sqrt{5}$=2.236,$\sqrt{50}$=7.071,则$\sqrt{0.5}$=0.7071,$\sqrt{500}$=22.36;
(3)$\root{3}{1}$=1,$\root{3}{1000}$=10,$\root{3}{1000000}$=100…
小数点变化的规律是:被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位.
(4)已知$\root{3}{10}$=2.154,$\root{3}{100}$=4.642,则$\root{3}{10000}$=21.54,$-\root{3}{0.1}$=-0.4642.
分析 (1)观察已知等式,得到一般性规律,写出即可;
(2)利用得出的规律计算即可得到结果;
(3)归纳总结得到规律,写出即可;
(4)利用得出的规律计算即可得到结果.
解答 解:(1)$\sqrt{2}$=1.414,$\sqrt{200}$=14.14,$\sqrt{20000}$=141.4…
$\sqrt{0.03}$=0.1732,$\sqrt{3}$=1.732,$\sqrt{300}$=17.32…
由此可见,被开方数的小数点每向右移动两位,其算术平方根的小数点向右移动一位;
(2)已知$\sqrt{5}$=2.236,$\sqrt{50}$=7.071,则$\sqrt{0.5}$=0.7071,$\sqrt{500}$=22.36;
(3)$\root{3}{1}$=1,$\root{3}{1000}$=10,$\root{3}{1000000}$=100…
小数点变化的规律是:被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;
(4)已知$\root{3}{10}$=2.154,$\root{3}{100}$=4.642,则$\root{3}{10000}$=21.54,$-\root{3}{0.1}$=-0.4642.
故答案为:(1)两;一;(2)0.7071;22.36;(3)被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;(4)21.54;-0.4642
点评 此题考查了立方根,以及算术平方根,弄清题中的规律是解本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
3.红细胞的平均直径是0.0000072m,用科学记数法表示为( )
| A. | 7.2×10-6 | B. | 7.2×106 | C. | 0.72×10-6 | D. | 7.2×10-5 |
5.下面给出了四边形ABCD的四内角关系中,能说明它是平行四边形的是( )
| A. | 1:2:3:4 | B. | 2:3:2:3 | C. | 2:2:3:3 | D. | 2:3:3:2 |
2.估算$\sqrt{18}$的值是在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
6.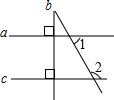 如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
 如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )
如图,已知在同一平面内的三条直线a,b,c,且a⊥b,b⊥c,若∠1=55°,则∠2的度数为( )| A. | 55° | B. | 125° | C. | 135° | D. | 无法确定 |
 如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)
如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)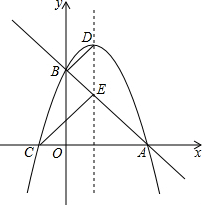 如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.
如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.