题目内容
18. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论:①b2-4ac>0,②a-2c>0,③2b+c>0,④a-2b+3c<0,⑤$\frac{a}{b}$-1=0,其中正确的有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据抛物线开口方向,对称轴的位置,与x轴交点个数,以及x=-1,x=1对应y值的正负判断即可.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,选项①正确;
∵抛物线开口向上,交y轴的负半轴,
∴a>0,c<0,
∴-2c>0,∴
a-2c>0,选项②正确;
∵x=-$\frac{1}{2}$,
∴-$\frac{b}{2a}$=-$\frac{1}{2}$,
∴b=a,∴$\frac{a}{b}$=1,
∴$\frac{a}{b}$-1=0,选项⑤正确;
∵当x=-1时,y<0,即a-b+c<0,当x=1时,y>0,即a-b+c<0,a+b+c>0,
∴2b+c>0,a-2b+3c=-b+3c<0,选项③④正确;
故选D.
点评 此题考查了二次函数图象与系数的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
8.下列命题:①内错角相等;②同旁内角互补;③直角都相等;④若n<1,则n2-1<0.其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.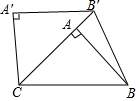 如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C、,点A在边B′C上,连结BB′,则∠ABB′的大小为24度.
如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C、,点A在边B′C上,连结BB′,则∠ABB′的大小为24度.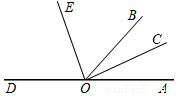 如图,已知点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=20°,求∠BOE的度数.
如图,已知点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=20°,求∠BOE的度数.