Question

7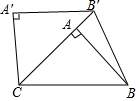．如图，在Rt△ABC中，∠BAC=90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C、，点A在边B′C上，连结BB′，则∠ABB′的大小为24度．

Answer 1

分析 由旋转的性质得到∠BCB′=48°，BC=B′C，根据等腰三角形的性质得到∠CBB′=$\frac{1}{2}$（180°-∠BCB′）=66°，根据余角的性质得到∠CBA=42°，于是得到结论．

解答 解：由旋转的性质得：∠BCB′=48°，BC=B′C，
∴∠CBB′=$\frac{1}{2}$（180°-∠BCB′）=66°，
∵∠BAC=90°，
∴∠CBA=42°，
∴∠ABB′=66°-42°=24°，
故答案为：24．

点评 本题考查了旋转的性质和直角三角形的性质，比较简单；明确旋转前后的两个角相等，及两直角三角形的两锐角互余．