题目内容
【题目】某班“数学兴趣小组”对函数y＝x2－2|x|的图象和性质进行了探究，探究过程如下：
(1)自变量x的取值范围是 ，x与y的几组对应值列表如下：
x | … | －3 | － | －2 | －1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | －1 | 0 | －1 | 0 |
| 3 | … |
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该图象的另一部分并观察函数图象，写出该函数的两条性质.
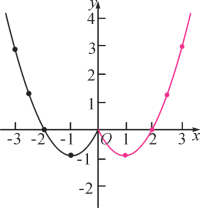
(3)进一步探究函数图象发现：关于x的方程2x2－4|x|＝a有4个实数根，则a的取值范围是 ．
【答案】（1）全体实数；（2）函数图象见解析；性质：①函数图象关于y轴对称；②当x＞1时，y随x的增大而增大；（3）－2＜a＜0.
【解析】
（1）由函数解析式可判断自变量x的取值范围；
（2）根据表格中数据描点、画图即可；根据函数图象可直接得出其性质；
（3）方程2x2－4|x|＝a有4个实数根，就是直线y＝
与y＝x2－2|x|的图象有4个交点，，根据函数图象求解即可．
解：（1）由函数解析式可知，自变量x的取值范围是全体实数，
故答案为：全体实数；
（2）函数图象如图所示：
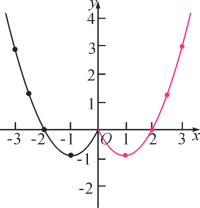
观察函数图象，可得出：
①函数图象关于y轴对称；
②当x＞1时，y随x的增大而增大；
（3）方程2x2－4|x|＝a可化简为x2－2|x|＝，
方程2x2－4|x|＝a有4个实数根时，即直线y＝与y＝x2－2|x|的图象有4个交点，
由函数图象可得：的取值范围是：－1＜＜0，
∴－2＜a＜0，
故答案为：－2＜a＜0．
练习册系列答案
相关题目
