题目内容
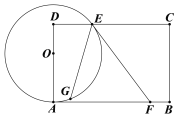
【题目】如图，O为矩形ABCD边AD上一点，以O为圆心，OA为半径画圆与CD交于点E，过点E作⊙O的切线EF交AB于F，点C关于EF的对称点G恰好落在⊙O上，若AD=4,AB=6,则OA的长为____．
【答案】
【解析】
连接OE，再过O点作GE垂线，交GE于点H，先证明
与
全等，得到DE=HE，利用对称得出GE=EC，再根据垂径定理（垂直于弦的直径平分这条弦）HE=HG,从而得出 DE的长，再设OA为x，在
中利用勾股定理建立方程求出OA的值即可
连接OE，再过O点作GE垂线，交GE于点H
由题意得：∠CEF=∠GEF，CE=GE
因为四边形ABCD为矩形
所以AD=BC=4, AB=CD=6, ∠A=∠B=∠C=∠D=90°
又因为EF是圆O切线
所以OE⊥EF,即∠OEF=90°
所以∠CEF＋∠DEO=∠GEF＋∠DEO=90°
所以∠DEO=∠OEH
又因为∠D=∠OHE=90°，OE=OE
所以
（AAS）
所以DE=HE=HG=
DC=
=2
设OA为x，则OD为4－x
在Rt
ODE中：
解得x=
故答案为
智能训练练测考系列答案
【题目】某班“数学兴趣小组”对函数y＝x2－2|x|的图象和性质进行了探究，探究过程如下：
(1)自变量x的取值范围是 ，x与y的几组对应值列表如下：
x | … | －3 | － | －2 | －1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | －1 | 0 | －1 | 0 |
| 3 | … |
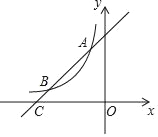
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该图象的另一部分并观察函数图象，写出该函数的两条性质.
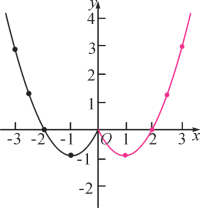
(3)进一步探究函数图象发现：关于x的方程2x2－4|x|＝a有4个实数根，则a的取值范围是 ．
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛．预先对这两名运动员进行了6次测试，成绩如下（单位：个）：
甲：6，12，8，12，10，12；
乙：9，10，11，10，12，8；
（1）填表：
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
（2）根据测试成绩，请你运用所学的统计知识作出分析，派哪一位运动员参赛更好？为什么？
