题目内容
1．一长方形菜地，面积为22㎡，对角线长10m，要在四周围上篱笆，则篱笆最少需要（ ）| A． | 30m | B． | 28m | C． | 26m | D． | 24m |
分析 首先设篱笆长为xm，则宽ym，由题意得：长×宽=22，长2+宽2=102，再利用完全平方公式可得x+y的值，然后可得答案．
解答 解：设篱笆长为xm，则宽ym，由题意得：
$\left\{\begin{array}{l}{xy=22}\\{{x}^{2}+{y}^{2}=100}\end{array}\right.$，
故（x+y）2=144，
则x+y=12，
篱笆最少需要：2（x+y）=28（m）．
故选：B．
点评 此题主要考查了勾股定理的应用，关键是正确理解题意，掌握直角三角形中两直角边的平方和等于斜边的平方．
练习册系列答案
相关题目
12．直线y=-2x+4与x轴、y轴的交点分别为A，B，点P（0，-2）是y轴上的一点，过点P作AB的垂线交x轴于点D，则点D的坐标为（ ）
| A． | （$\frac{5}{2}$，0） | B． | （3，0） | C． | （4，0） | D． | （5，0） |
9．两个相似多边形的相似比是3：4，其中较小的多边形周长是36，则较大多边形的周长为（ ）
| A． | 48 | B． | 54 | C． | 56 | D． | 64 |
如图，MN是线段AB的中垂线，MN=6，在MN上取C、D两点，连接AD，AC，BC，S△BMN：S△ADN=2：1，S△ADN：S△BCN=4：3，则CD的长度为$\frac{3}{4}$．
6．
如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是（ ）
如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
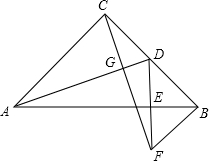如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．
如图，D在AB上，AB=AC
如图，要从小河引水到村庄A，请先作出最佳路线，再写出理由：垂线段最短．