Question

13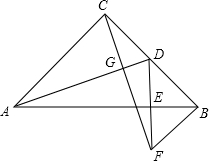．如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．
（1）求证：CD=BF；
（2）求证：AD⊥CF；
（3）连接AF，试判断△ACF的形状．

Answer 1

分析 （1）由平行可求得∠CBF=90°，再结合等腰三角形的判定和性质可求得BF=BD，可得BF=CD；
（2）结合（1）的结论，可证明△ACD≌△CBF，可得∠DCG=∠CAD，可证明∠CGD=90°，可得结论；
（3）由（2）可得CF=AD，又AB垂直平分DF，可得AD=AF，可证明CF=AF，可知△ACF为等腰三角形．

解答 （1）证明：
∵AC∥BF，且∠ACB=90°，
∴∠CBF=90°，
又AC=BC，
∴∠DBA=45°，
∵DE⊥AB，
∴∠DEB=∠BEF=∠DBF=90°，
∴∠BDE=∠BFE=45°，
∴BD=BF，
又D为BC中点，
∴CD=BD，
∴CD=BF；
（2）证明：
由（1）可知CD=BF，且CA=CB，∠ACB=∠CBF=90°，
在△ACD和△CBF中
$\left\{\begin{array}{l}{CD=BF}\\{∠ACD=∠CBF}\\{AC=BC}\end{array}\right.$
∴△ACD≌△CFB（SAS），
∴∠CAD=∠BCF，
∵∠ACB=90°，
∴∠CAD+∠CDA=90°，
∴∠BCF+∠CDA=90°，
∴∠CGD=90°，
∴AD⊥CF；
（3）解：
由（2）可知△ACD≌△CBF，
∴AD=CF，
由（1）可知AB垂直平分DF，
∴AD=AF，
∴AF=CF，
∴△ACF为等腰三角形．

点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（SSS、SAS、ASA、AAS和HL）和性质（全等三角形的对应边、对应角相等）是解题的关键．