题目内容
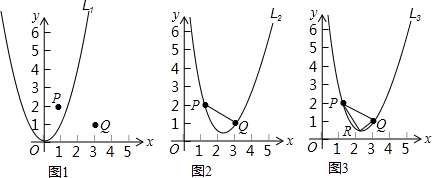
6．
如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
分析 根据圆周角定理，可得∠AED与∠ABD的关系，根据勾股定理，可得BC的长，再根据余弦等于邻边比斜边，可得答案．
解答 解：由圆周角定理，得
∠AED=∠ABD．
在Rt△ABC中，由勾股定理，得
BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{5}$，
cos∠AED=cos∠ABC=$\frac{AB}{BC}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$，
故选：D．
点评 本题考查了锐角三角函数的定义，利用圆周角定理得出∠AED=∠ABD是解题关键，注意余弦是在直角三角形中邻边比斜边．
练习册系列答案
相关题目
17．
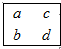如图是2012年11月份的日历，现用一长方形在日历中任意框出4个数，请用一个等式表示a，b，c，d之间的关系，下列表示正确的是（ ）
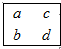如图是2012年11月份的日历，现用一长方形在日历中任意框出4个数，请用一个等式表示a，b，c，d之间的关系，下列表示正确的是（ ）| A． | a+d=b+c | B． | a+c=b+d | C． | a+b=c+d | D． | a+d+1=b+c |
14．
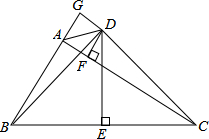如图，在△ABC中，AC＞AB，DE（点D在△ABC的外部）垂直平分BC，交BC于点E，连接BD，CD，AD，过点D作DF⊥AC于点F，延长BA到点G，使得BG=CF，连接DG，若∠DBC-∠GBD=∠BCA，则下列说法中不正确的是（ ）
如图，在△ABC中，AC＞AB，DE（点D在△ABC的外部）垂直平分BC，交BC于点E，连接BD，CD，AD，过点D作DF⊥AC于点F，延长BA到点G，使得BG=CF，连接DG，若∠DBC-∠GBD=∠BCA，则下列说法中不正确的是（ ）| A． | ∠BGD=90° | B． | AD平分∠GAC | C． | ∠GDB=∠FDC | D． | ∠BDG=90° |
1．一长方形菜地，面积为22㎡，对角线长10m，要在四周围上篱笆，则篱笆最少需要（ ）
| A． | 30m | B． | 28m | C． | 26m | D． | 24m |
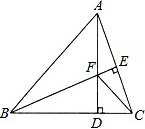△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC，∠BAD=45°，AD与BE交于点F，连接CF，
甲乙两人住的房间号都是三位数的完全平方数，当他们将自己的房间号写下来并排成形状时，他们惊呆了，这个数阵中每列（自上而下）两数组成的两位数也是完全平方数．请说说：他们各自房间号码是多少？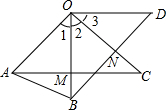
已知，OA=OB，OC=OD，∠1=∠2=∠3，AC交OB于M，BD交OC于N，求证：OM=ON．