题目内容
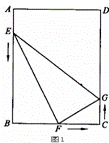
如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别 从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,
从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时, 三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。
三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。



(1)当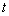
 =1s时,S的值是多少?
=1s时,S的值是多少?
(2) 当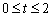
 时,点E、F、G分别在边AB、BC、CD上移动,用含
时,点E、F、G分别在边AB、BC、CD上移动,用含 t的代
t的代 数式表示S;当
数式表示S;当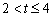
 时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
(3)若点F在矩形的边BC上移动,当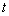
 为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由
为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似?请说明理由

(2)①如图1,当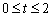
 时,点E、F、G分别在边AB、BC、CD
时,点E、F、G分别在边AB、BC、CD
上移动,此时





即
 (
(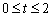
 ). (5分)
). (5分)
②如图2当点F追上点G时,
 ,解得
,解得
 。
。
当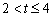
 时,点E
时,点E 在边AB上移动,点F、G都在边CD上移动,
在边AB上移动,点F、G都在边CD上移动,
此时CF=
 .CG=
.CG=
 ,FG=CG-CF=
,FG=CG-CF=
 .
.



 (
(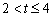
 ) (7分)
) (7分)
(3)如图1,当点F在矩形的边BC上移动时,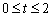
 .
.
在△EBF和△FCG中,∠B=∠C=90°,
①若
 .即
.即
 ,解得
,解得
 , (10分)
, (10分)
又
 满足
满足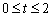
 ,所以当
,所以当
 时,△EBF∽△FCG,
时,△EBF∽△FCG,


 (14分)
(14分)
考点:1.相似三角形的判定;2.一次函数的应用;3.三角形的面积;4.矩形的性质.

练习册系列答案
相关题目
 AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
 8cm,BC=4cm,D、E分别为边AB、BC的中点
8cm,BC=4cm,D、E分别为边AB、BC的中点 ,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
 cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s). 长为______cm,(用含t的代数式表示).
长为______cm,(用含t的代数式表示). 度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.
度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围. C中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线
C中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线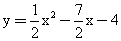 经过
经过 A、B两点。若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点
A、B两点。若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点 P,连结PA、P
P,连结PA、P B.设直线l移动的时间为t(0<t<4
B.设直线l移动的时间为t(0<t<4 )秒,求四
)秒,求四 边形PBCA的面积S(面
边形PBCA的面积S(面 积单
积单 位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积。
位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积。
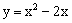 经过点A,B及原点O,顶点为C,直线OB为
经过点A,B及原点O,顶点为C,直线OB为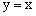 ,点P是抛物线上的动点,过点P作PM⊥x轴,
,点P是抛物线上的动点,过点P作PM⊥x轴, 垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.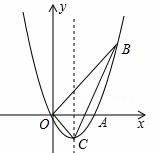
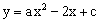 (a,c为常数)的顶点为P,
(a,c为常数)的顶点为P, 等腰直角三角形ABC的顶点A的坐标
等腰直角三角形ABC的顶点A的坐标 为(0,﹣1),C的坐标为(﹣4,3),
为(0,﹣1),C的坐标为(﹣4,3),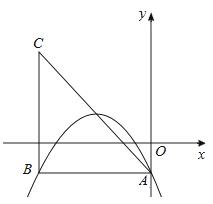
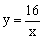 在第一象限内的图象经过点A,与
在第一象限内的图象经过点A,与 BC交于点F,OB=
BC交于点F,OB=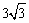 ,BF=
,BF=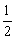 BC。过
BC。过 点F作EF∥OB,交OA于点,点
点F作EF∥OB,交OA于点,点 直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。
直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。 
 B是⊙O的一条弦,点C是⊙O优弧AB上一动点,且∠ACB=45°,点E
B是⊙O的一条弦,点C是⊙O优弧AB上一动点,且∠ACB=45°,点E 、F分别是AC、BC的中点,直线EF与⊙O交于G、
、F分别是AC、BC的中点,直线EF与⊙O交于G、 H两点,若⊙O的半径为7,则GE+FH的最大值为 .
H两点,若⊙O的半径为7,则GE+FH的最大值为 .
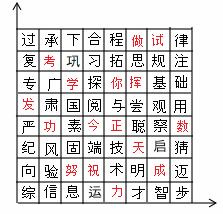
 做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。
做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。