题目内容
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数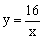 在第一象限内的图象经过点A,与
在第一象限内的图象经过点A,与 BC交于点F,OB=
BC交于点F,OB=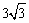 ,BF=
,BF=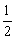 BC。过
BC。过 点F作EF∥OB,交OA于点,点
点F作EF∥OB,交OA于点,点 P为
P为 直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。
直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。

解:∵点A是反比例 函数
函数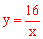 在第一象限内的图象上的点,
在第一象限内的图象上的点,
 ∴可设A
∴可设A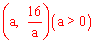 。
。
∵四边形OACB是平行四边形 , BF=
, BF=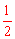 BC,∴F
BC,∴F 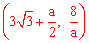
 。
。
∵点F是反比例函数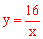 在第一象限内的图象上的点,
在第一象限内的图象上的点,
∴ 。
。
∴A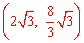 ,
, F
F 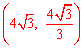 。
。
 ∵EF∥O
∵EF∥O B,点P为直线EF上的一个动点,∴可设P
B,点P为直线EF上的一个动点,∴可设P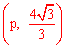 。
。
根据勾股定理,得OA2= ,OP2=
,OP2=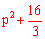 ,AP2=
,AP2=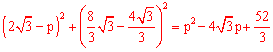 。
。
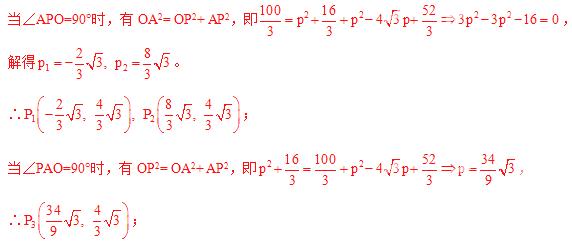
当∠POA=90°时,有AP2= OA2+ OP2,即
OP2,即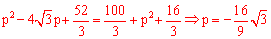 ,
,
∴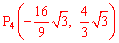 。
。
综上所述,满足条件的点P 的坐标为
的坐标为 ,
,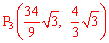 ,
,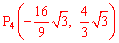 。
。
【考点】反比 例函数综合题,单动点问题,曲线上点的坐标与方程的
例函数综合题,单动点问题,曲线上点的坐标与方程的 关系,平行四边形的性质,勾股定理,直角三角形的判定,分类思想和数形结合思想的应用。
关系,平行四边形的性质,勾股定理,直角三角形的判定,分类思想和数形结合思想的应用。
【解析】先根据曲线上点的坐标与方程的关系 和平行四边形的性质求出点A,F的坐标,再分别根据当∠
和平行四边形的性质求出点A,F的坐标,再分别根据当∠ APO=90°时,在OA的两侧各有一点P,得出P1,P2;当∠PAO=
APO=90°时,在OA的两侧各有一点P,得出P1,P2;当∠PAO= 90°时,求出P3;当∠POA=90°时,求出P4即可。
90°时,求出P3;当∠POA=90°时,求出P4即可。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
F∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2. ,B两点)时,求S与t之间的函数关系式.
,B两点)时,求S与t之间的函数关系式.
 D中,AH⊥DC,垂足为H,AB=
D中,AH⊥DC,垂足为H,AB=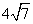 ,AD=7,AH=
,AD=7,AH=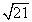 . 现有两个动点
. 现有两个动点 E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运
E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运 动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
动到点C时,E、F两点同时停止运动. 设运转时间为t秒. 的面积为S,请直接写出S与t之间的函数关系式
的面积为S,请直接写出S与t之间的函数关系式 ,并写出相应的自变量t的取值范围;
,并写出相应的自变量t的取值范围; . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射 线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.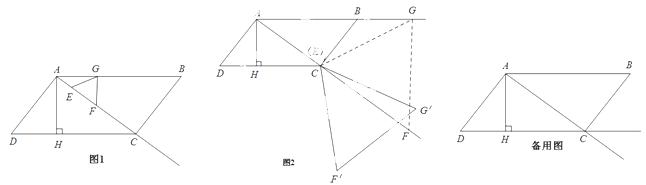
 从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,
从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时, 三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。
三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2。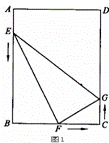



 =1s时,S的值是多少?
=1s时,S的值是多少?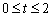
 时,点E、F、G分别在边AB、BC、CD上移动,用含
时,点E、F、G分别在边AB、BC、CD上移动,用含 t的代
t的代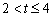
 与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置.
与x轴交于点A,将线段OA绕点O逆时针旋转1200至OB的位置. 的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.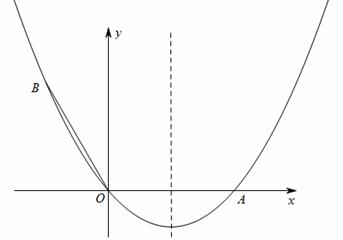
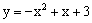 上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC
上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC =
=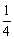 MP,MD=
MP,MD=
 别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与
别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与 BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10)。
BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10)。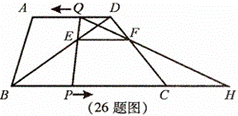

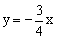 上一点,则点B与其对应点B′间的距离为【 】
上一点,则点B与其对应点B′间的距离为【 】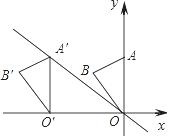
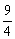 B.3 C.4
B.3 C.4  D.5
D.5 14个半径为r的圆紧密排列成一条直线,半径为r
14个半径为r的圆紧密排列成一条直线,半径为r 的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周
的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周