题目内容
13.在△ABC中,∠C=90°,(1)若BC=5,AC=12,则AB=13;
(2)若BC=3,AB=5,则AC=4;
(3)若BC:AC=3:4,AB=10,则BC=6,AC=8.
(4)若AB=8.5,AC=7.5,则BC=4.
分析 (1)由勾股定理求出AB即可;
(2)由勾股定理求出AC即可;
(3)由勾股定理求出AB=5x=10,求出x=2,即可得出BC和AC的长;
(4)由勾股定理求出BC即可.
解答 解:(1)在△ABC中,∠C=90°,根据勾股定理可得:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13;
故答案为:13;
(2)在△ABC中,∠C=90°,根据勾股定理可得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
故答案为:4;
(3)∵BC:AC=3:4,
∴设BC=3x,则AC=4x,
在△ABC中,∠C=90°,根据勾股定理可得:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=5x=10,
∴x=2,
∴BC=6,AC=8;
故答案为:6,8;
(4)在△ABC中,∠C=90°,根据勾股定理可得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{8.{5}^{2}-7.{5}^{2}}$=4;
故答案为:4.
点评 此题主要考查了勾股定理,关键是掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
3.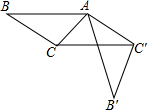 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )| A. | 138 | B. | 128 | C. | 118 | D. | 108 |
