题目内容
14．
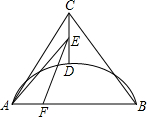如图，AC=BC，点D是以线段AB为弦的圆弧的中点，AB=4，点E、F分别是线段CD，AB上的动点．设AF=x，AE2-FE2=y，则能表示y与x的函数关系的图象是（ ）| A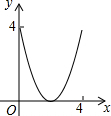． |  | B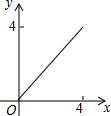． |  | C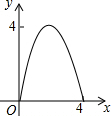． |  | D． |  |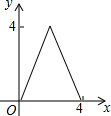
分析 延长CE交AB于G，△AEG和△FEG都是直角三角形，运用勾股定理列出y与x的函数关系式即可判断出函数图象．
解答 
解：如右图所示，延长CE交AB于G．设AF=x，AE2-FE2=y；
∵△AEG和△FEG都是直角三角形
∴由勾股定理得：AE2=AG2+GE2，FE2=FG2+EG2，
∴AE2-FE2=AG2-FG2，即y=22-（2-x）2=-x2+4x，
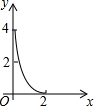
这个函数是一个二次函数，抛物线的开口向下，对称轴为x=2，与x轴的两个交点坐标分别是（0，0），（4，0），顶点为（2，4），自变量0＜x＜4．
所以C选项中的函数图象与之对应．
故选C．
点评 本题考查了动点问题的函数图象，解决有关动点问题的函数图象类习题时，关键是要根据条件找到所给的两个变量之间的函数关系，尤其是在几何问题中，更要注意基本性质的掌握和灵活运用．
练习册系列答案
相关题目
如图是什么几何体的展开图？
2．（a+b-c）（a-b-c）=[a+□][a-□]，□里所填的各项分别是（ ）
| A． | b-c，b+c | B． | -b+c，b-c | C． | b-c，b-c | D． | -b+c，b+c |
如图，在Rt△ABC中，∠C=90°，AC=2，BC=4，点P是线段AC上的一动点，过点P作PQ∥AB交BC于点Q．设AP=x，S△PCQ=y，则y关于x的函数图象大致是（ ）
6．下列说法中，正确的是（ ）
| A． | 单项式4a+$\frac{1}{b}$m的次数是0 | |
| B． | $\frac{1}{x}$是整式 | |
| C． | -$\frac{1}{4}$不是单项式 | |
| D． | 单项式-$\frac{{{2^3}mn}}{8}$的系数是-1，次数是2 |
3．若2x2y1-2m和3xn-1y2是同类项，则mn的值是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{8}$ | D． | -$\frac{1}{8}$ |
4．有下列长度的三条线段，能组成三角形的一组是（ ）
| A． | 5cm、3cm、4cm | B． | 1cm、1cm、2cm | C． | 1cm、2cm、3cm | D． | 6cm、10cm、3cm |