题目内容
10.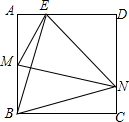 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )| A. | 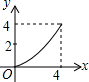 | B. | 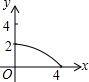 | C. | 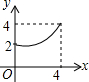 | D. | 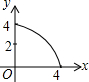 |
分析 根据垂直平分线的性质得到BM=EM=y,求得AM=4-y,根据勾股定理列方程即可得到结论.
解答 解:∵ BE的中垂线交AB于点M,交DC于点N,
BE的中垂线交AB于点M,交DC于点N,
∴BM=EM=y,
∵AB=4,
∴AM=4-y,
∵四边形ABCD为正方形,
∴∠A=90°,
∴AM2+AE2=EM2,
即(4-y)2+x2=y2,
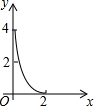
∴y=$\frac{1}{8}$x2+2,
根据二次函数的图形和性质,这个函数的图形是开口向上,对称轴是y轴,顶点是(0,2),自变量的取值范围是0<x<4.
故选C.
点评 本题考查的是动点问题的函数图象,先根据正方形的性质得到BE=MN,然后表示出y关于x的二次函数,确定二次函数的大致图象.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
2.(a+b-c)(a-b-c)=[a+□][a-□],□里所填的各项分别是( )
| A. | b-c,b+c | B. | -b+c,b-c | C. | b-c,b-c | D. | -b+c,b+c |
20.下列命题正确的是( )
| A. | 到角两边距离相等的点在这个角的平分线上 | |
| B. | 垂直于同一条直线的两条直线互相平行 | |
| C. | 平行于同一条直线的两条直线互相平行 | |
| D. | 等腰三角形的高线、角平分线、中线互相重合 |
 证明题:如图,AB=DC,AC=DB,AC和DB相交于O
证明题:如图,AB=DC,AC=DB,AC和DB相交于O 如图是什么几何体的展开图?
如图是什么几何体的展开图? 如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )