题目内容
1. 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求$\widehat{DE}$的长.
分析 (1)过点C作AB的垂线,垂足为点D,然后以C点为圆心,CD为半径作圆即可;
(2)先根据切线的性质得∠ADC=90°,则利用互余可计算出∠DCE=90°-∠A=60°,∠BCD=90°-∠ACD=30°,再在Rt△BCD中利用∠BCD的余弦可计算出CD=$\frac{3\sqrt{3}}{2}$,然后根据弧长公式求解.
解答 解:(1)如图,
⊙C为所求;
(2)∵⊙C切AB于D,
∴CD⊥AB,
∴∠ADC=90°,
∴∠DCE=90°-∠A=90°-30°=60°,
∴∠BCD=90°-∠ACD=30°,
在Rt△BCD中,∵cos∠BCD=$\frac{CD}{BC}$,
∴CD=3cos30°=$\frac{3\sqrt{3}}{2}$,
∴$\widehat{DE}$的长=$\frac{60•π•\frac{3\sqrt{3}}{2}}{180}$=$\frac{\sqrt{3}}{2}$π.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的性质和弧长公式.

练习册系列答案
相关题目
12. 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
16.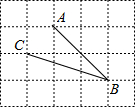 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
6.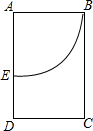 在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
 在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )| A. | 4 | B. | 16 | C. | 4$\sqrt{2}$ | D. | 8 |
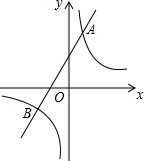 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
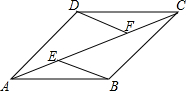 已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.