题目内容
 如图所示,在ABC中,AB=AC=BC,点D、E、F分别在BC、CA边延长线上,BE=AF=CD.求证:△DEF是等边三角形.
如图所示,在ABC中,AB=AC=BC,点D、E、F分别在BC、CA边延长线上,BE=AF=CD.求证:△DEF是等边三角形.考点:等边三角形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:由条件可得△ABC为等边三角形,结合BE=AF=CD证明△AEF≌△CFD≌△BDE即可.
解答:证明:∵AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=∠ABC=60°,
∴∠EAF=∠EBD=120°,
∵BE=AF,
∴BE+AB=FA+AC,即AE=CF,
在△AEF和△BDE中,
,
∴△AEF≌△BDE(SAS),
∴EF=ED,
同理可得△AEF≌△CFD,
∴EF=FD,
∴EF=ED=FD,
∴△DEF为等边三角形.
∴△ABC为等边三角形,
∴∠BAC=∠ABC=60°,
∴∠EAF=∠EBD=120°,
∵BE=AF,
∴BE+AB=FA+AC,即AE=CF,
在△AEF和△BDE中,
|
∴△AEF≌△BDE(SAS),
∴EF=ED,
同理可得△AEF≌△CFD,
∴EF=FD,
∴EF=ED=FD,
∴△DEF为等边三角形.
点评:本题主要考查等边三角形的性质和判定,掌握其判定方法是解题的关键.

练习册系列答案
相关题目
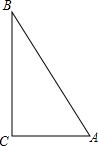 如图,在Rt△ABC中,∠C=90°,AB=3AC,
如图,在Rt△ABC中,∠C=90°,AB=3AC,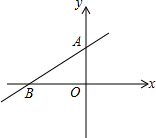 已知一次函数y=(a-1)x+2(a-1)(a≠1)的图象如图所示,已知3OA=2OB,求一次函数的解析式.
已知一次函数y=(a-1)x+2(a-1)(a≠1)的图象如图所示,已知3OA=2OB,求一次函数的解析式.