题目内容
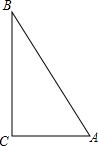如图，在Rt△ABC中，∠C=90°，AB=3AC，（1）求sinA，sinB，cosA，cosB的值；
（2）从上面的计算中你发现什么规律．
考点：解直角三角形
专题：规律型
分析：（1）设AC=x，则AB=3x，根据勾股定理计算出BC=2
x，然后根据锐角三角函数的定义求解；
（2）根据（1）的计算结论可得到锐角三角函数中的互余公式．
| 2 |
（2）根据（1）的计算结论可得到锐角三角函数中的互余公式．
解答：解：（1）设AC=x，则AB=3x，
所以BC=
=2
x，
所以sinA=
=
=
，sinB=
=
=
，cosA=
=
，cosB=
=
；
（2）当∠A+∠B=90°时，
则sinA=cosB，cosA=sinB．
所以BC=
| AB2-AC2 |
| 2 |
所以sinA=
| BC |
| AB |
2
| ||
| 3x |
2
| ||
| 3 |
| AC |
| AB |
| x |
| 3x |
| 1 |
| 3 |
| AC |
| AB |
| 1 |
| 3 |
| BC |
| AB |
2
| ||
| 3 |
（2）当∠A+∠B=90°时，
则sinA=cosB，cosA=sinB．
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
相关题目
如图，在平面直角坐标系中，A（1，2），B（3，1），C（-2，-1）．
如图所示，在ABC中，AB=AC=BC，点D、E、F分别在BC、CA边延长线上，BE=AF=CD．求证：△DEF是等边三角形．