题目内容
1.下列运算正确的是( )| A. | (2x3y)2=4x6y2 | B. | $\sqrt{(-4)×(-6)}$=$\sqrt{-4}$×$\sqrt{-6}$ | C. | x8÷x4=x2 | D. | -16(x-2)=-16x-32 |
分析 根据幂的乘方法则:底数不变,指数相乘;积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘;二次根式中的被开方数是非负数;同底数幂的除法法则:底数不变,指数相减;去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反分别进行分析即可.
解答 解:A、(2x3y)2=4x6y2,计算正确;
B、$\sqrt{(-4)×(-6)}$=$\sqrt{-4}$×$\sqrt{-6}$,计算错误,应为$\sqrt{(-4)×(-6)}$=$\sqrt{4×6}$=2$\sqrt{6}$;
C、x8÷x4=x2,计算错误,应为x8÷x4=x4;
D、-16(x-2)=-16x-32,计算错误,应为-16(x-2)=-16x+32;
故选:A.
点评 此题主要考查了二次根式有意义、同底数幂的除法、幂的乘方、积的乘方,以及去括号法则,关键是熟练掌握各知识点和计算法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,是反比例函数y1=$\frac{k}{x}$和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是( )
如图,是反比例函数y1=$\frac{k}{x}$和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是( )
 如图,是反比例函数y1=$\frac{k}{x}$和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是( )
如图,是反比例函数y1=$\frac{k}{x}$和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是( )| A. | 1<x<6 | B. | x<1 | C. | x<6 | D. | x>1 |
6.某工厂接到加工600件衣服的订单,预计每天做25件,正好按时完成,后因客户要求提前3天交货,工人则需要提高每天的工作效率,设工人每天应多做x件,依题意列方程正确的是( )
| A. | $\frac{600}{25+x}$-$\frac{600}{25}$=3 | B. | $\frac{600}{25}$+3=$\frac{600}{x}$ | C. | $\frac{600}{25}$-$\frac{600}{x}$=3 | D. | $\frac{600}{25}$-$\frac{600}{25+x}$=3 |
13.-2017的倒数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -$\frac{1}{2017}$ | D. | 0 |
10.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )
| A. | m≥-1 | B. | m>-1 | C. | m≤-1 | D. | m<-1 |
 点A、B、C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是$\frac{3\sqrt{5}}{5}$.
点A、B、C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是$\frac{3\sqrt{5}}{5}$.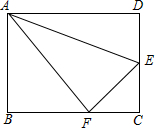 如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°
如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°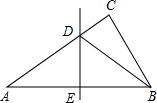 如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( )
如图,在△ABC中,DE垂直平分AB,交边AC于点D,交边AB于点E,连接BD.若AC=6,△BCD的周长为10,则BC的长为( )