题目内容
9.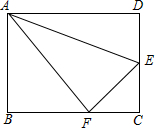 如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°
如图,在矩形ABCD中,AB=6,AD=8,点E,F分别是边CD,BC上的动点,且∠AFE=90°(1)证明:△ABF∽△FCE;
(2)当DE取何值时,∠AED最大.
分析 (1)根据等角的余角相等,证明∠AFB=∠FEC即可解决问题;
(2)取AE的中点O,连接OD、OF.由∠AFE=∠ADE=90°,可知OA=OD=OE=OF,推出A、D、E、F四点共圆,推出∠AED=∠AFD,推出当⊙O与BC相切时,∠AFD的值最大,易知BF=CF=4,由△ABF∽△FCE,可得$\frac{AB}{FC}$=$\frac{BF}{EC}$,求出EC即可解决问题;
解答 (1)证明: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AFE=90°,
∴∠AFB+∠EFC=90°,∵∠EFC+∠FEC=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)取AE的中点O,连接OD、OF.
∵∠AFE=∠ADE=90°,
∴OA=OD=OE=OF,
∴A、D、E、F四点共圆,
∴∠AED=∠AFD,
∴当⊙O与BC相切时,∠AFD的值最大,易知BF=CF=4,
∵△ABF∽△FCE,
∴$\frac{AB}{FC}$=$\frac{BF}{EC}$,
∴$\frac{6}{4}$=$\frac{4}{EC}$,
∴EC=$\frac{8}{3}$,
∴DE=DC-CE=6-$\frac{8}{3}$=$\frac{10}{3}$.
∴当DE=$\frac{10}{3}$时,∠AED的值最大.
点评 本题考查相似三角形的性质与判定、矩形的性质、圆的有关知识,解题的关键是学会添加辅助圆解决问题,属于中考压轴题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.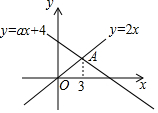 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )| A. | x≥$\frac{3}{2}$ | B. | x≥3 | C. | x$≤\frac{3}{2}$ | D. | x≤3 |
10. 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
1.下列运算正确的是( )
| A. | (2x3y)2=4x6y2 | B. | $\sqrt{(-4)×(-6)}$=$\sqrt{-4}$×$\sqrt{-6}$ | C. | x8÷x4=x2 | D. | -16(x-2)=-16x-32 |
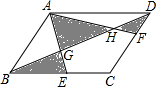 如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?
如图,在平行四边形ABCD中,BE=EC,CF=2FD.求阴影面积和空白面积的比?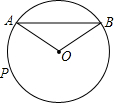 如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°
如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°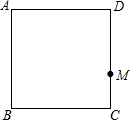 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.