题目内容
4. 点A、B、C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是$\frac{3\sqrt{5}}{5}$.
点A、B、C在格点图中的位置如图5所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离是$\frac{3\sqrt{5}}{5}$.
分析 连接AC,BC,设点C到线段AB所在直线的距离是h,利用勾股定理求出AB的长,利用三角形的面积公式即可得出结论.
解答  解:连接AC,BC,设点C到线段AB所在直线的距离是h,
解:连接AC,BC,设点C到线段AB所在直线的距离是h,
∵S△ABC=3×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×3-1=9-1-1-$\frac{9}{2}$-1=$\frac{3}{2}$,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴$\frac{1}{2}$×$\sqrt{5}$h=$\frac{3}{2}$,
∴h=$\frac{3\sqrt{5}}{5}$.
故答案为:$\frac{3\sqrt{5}}{5}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
15.掷一枚质地均匀的骰子一次出现下列事件,其中的必然事件为( )
| A. | 掷出的点数是1 | B. | 掷出的点数是偶数 | ||
| C. | 掷出的点数是奇数 | D. | 掷出的点数小于7 |
12.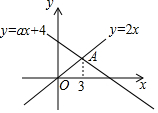 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(3,m),则不等式2x≥ax+4的解集为( )| A. | x≥$\frac{3}{2}$ | B. | x≥3 | C. | x$≤\frac{3}{2}$ | D. | x≤3 |
19.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9. 下面长方体的主视图(主视图也称正视图)是( )
下面长方体的主视图(主视图也称正视图)是( )
 下面长方体的主视图(主视图也称正视图)是( )
下面长方体的主视图(主视图也称正视图)是( )| A. |  | B. |  | C. |  | D. |  |
16.下列运算正确的有( )
| A. | 5ab-ab=4 | B. | (a2)3=a6 | C. | (a-b)2=a2-b2 | D. | $\sqrt{9}$=±3 |
1.下列运算正确的是( )
| A. | (2x3y)2=4x6y2 | B. | $\sqrt{(-4)×(-6)}$=$\sqrt{-4}$×$\sqrt{-6}$ | C. | x8÷x4=x2 | D. | -16(x-2)=-16x-32 |