题目内容
9.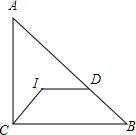 如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连接CI,则∠CID=135°.
如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连接CI,则∠CID=135°.
分析 由I为Rt△ABC的内心,得出CI平分∠ACB,求出∠BCI=$\frac{1}{2}$∠ACB=45°,由平行线的性质得出同旁内角互补,即可得出结果.
解答 解:∵∠ACB=90°,I为Rt△ABC的内心,
∴CI平分∠ACB,
∴∠BCI=$\frac{1}{2}$∠ACB=45°,
∵ID∥BC,
∴∠CID+∠BCI=180°,
∴∠CID=180°-45°=135°;
故答案为:135.
点评 本题考查了三角形的内心的性质、角平分线的定义、平行线的性质;熟记三角形的内心性质是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.
如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.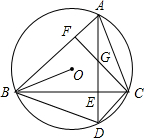 如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.
如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.
 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.求证:AC•AD=AB•AE.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.求证:AC•AD=AB•AE.