题目内容
17.因式分解(1)ab2-4a
(2)3x3y-6x2y2+3xy3.
分析 (1)原式提取公因式,再利用平方差公式分解即可;
(2)原式提取公因式,再利用完全平方公式分解即可.
解答 解:(1)原式=a(b2-4)=a(b+2)(b-2);
(2)原式=3xy(x2-2xy+y2)=3xy(x-y)2.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如果10b=n,那么称b为n的劳格数,记为b=d (n),由定义可知:10b=n与b=d (n)所表示的是b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
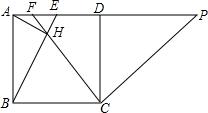 如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$.
如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$. 如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=52°,CE⊥AD,则∠DCE的度数是64°.
如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=52°,CE⊥AD,则∠DCE的度数是64°.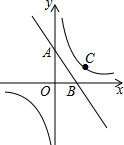 如图,A(0,4),B(3,0),C(4,2),且反比例函数图象经过点C.
如图,A(0,4),B(3,0),C(4,2),且反比例函数图象经过点C.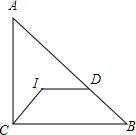 如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连接CI,则∠CID=135°.
如图,在Rt△ABC中,∠ACB=90°,I为Rt△ABC的内心,过点I作ID∥BC,交斜边AB于点D,连接CI,则∠CID=135°.