Question

20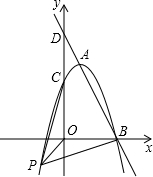．如图，已知直线y=kx+6与抛物线y=ax²+bx+c相交于A，B两点，且点A（1，4）为抛物线的顶点，点B在x轴上．
（1）求抛物线的解析式；
（2）在（1）中抛物线的第三象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；
（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．

Answer 1

分析 （1）由待定系数法确定函数解析式；
（2）先确定出点C坐标，再由△POB≌△POC建立方程，求解即可，
（3）分三种情况计算，分别判断△DAQ₁∽△DOB，△BOQ₂∽△DOB，△BOQ₃∽△Q₃EA，列出比例式建立方程求解即可．

解答 解：（1）把A（1，4）代入y=kx+6，
∴k=-2，
∴y=-2x+6，
由y=-2x+6=0，得x=3
∴B（3，0）．
∵A为顶点
∴设抛物线的解析为y=a（x-1）²+4，
∴a=-1，
∴y=-（x-1）²+4=-x²+2x+3      
（2）存在．
当x=0时y=-x²+2x+3=3，
∴C（0，3）
∵OB=OC=3，OP=OP，
∴当∠POB=∠POC时，△POB≌△POC，
作PM⊥x轴于M，作PN⊥y轴于N，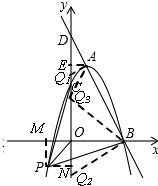
∴∠POM=∠PON=45°．
∴PM=PN      
∴设P（m，m），则m=-m²+2m+3，
∴m=$\frac{{1±\sqrt{13}}}{2}$，
∵点P在第三象限，
∴P（$\frac{{1-\sqrt{13}}}{2}$，$\frac{{1-\sqrt{13}}}{2}$）．   
（3）①如图，当∠Q₁AB=90°时，作AE⊥y轴于E，
∴E（0，4）
∵∠DA Q₁=∠DOB=90°，∠AD Q₁=∠BDO
∴△DAQ₁∽△DOB，
∴$\frac{AD}{OD}=\frac{{D{Q_1}}}{DB}$，即$\frac{{\sqrt{{1^2}+{{（6-4）}^2}}}}{6}=\frac{{D{Q_1}}}{{\sqrt{{3^2}+{6^2}}}}$，
∴DQ₁=$\frac{5}{2}$，
∴OQ₁=$\frac{7}{2}$，
∴Q₁（0，$\frac{7}{2}$）；     
②如图，
当∠Q₂BA=90°时，∠DBO+∠OBQ₂=∠OBQ₂+∠O Q₂B=90°
∴∠DBO=∠O Q₂B
∵∠DOB=∠B O Q₂=90°
∴△BOQ₂∽△DOB，
∴$\frac{OB}{OD}=\frac{{O{Q_2}}}{OB}$，
∴$\frac{3}{6}=\frac{{O{Q_2}}}{3}$，
∴OQ₂=$\frac{3}{2}$，
∴Q₂（0，$-\frac{3}{2}$）；     
③如图，当∠AQ₃B=90°时，∠AEQ₃=∠BOQ₃=90°，
∴∠AQ₃E+∠E AQ₃=∠AQ₃E+∠B Q₃O=90°
∴∠E AQ₃=∠B Q₃O
∴△BOQ₃∽△Q₃EA，
∴$\frac{OB}{{{Q_3}E}}=\frac{{O{Q_3}}}{AE}$，即$\frac{3}{{4-O{Q_3}}}=\frac{{O{Q_3}}}{1}$，
∴OQ₃²-4OQ₃+3=0，
∴OQ₃=1或3，
∴Q₃（0，1）或（0，3）．      
综上，Q点坐标为（0，$\frac{7}{2}$）或（0，$-\frac{3}{2}$）或（0，1）或（0，3）．

点评 此题是二次函数综合题，主要考查了待定系数法求函数解析式，全等三角形的性质，相似三角形的性质和判定，解本题的关键是判断三角形相似．