题目内容
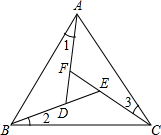 如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.
如图,已知在△ABC中,∠BAC=∠ACB=∠CBA,∠1=∠2=∠3.(1)△DEF是等边三角形吗?为什么?
(2)写出图中的全等三角形并说明你的理由.
考点:全等三角形的判定,等腰三角形的判定
专题:
分析:(1)由条件可知△ABC为等边三角形,结合条件可证明△ABD≌△CAF≌△BCE,可得到DE=EF=FD,可得△DEF为等边三角形;
(2)由(1)的过程可得出△ABD≌△CAF≌△BCE,证明过程同(1).
(2)由(1)的过程可得出△ABD≌△CAF≌△BCE,证明过程同(1).
解答:解:(1)∵∠BAC=∠ACB=∠CBA,
∴△ABC为等边三角形,
∴AB=BC=AC,
∵∠1=∠2=∠3,
∴∠ABD=∠CAF=∠BCE,
在△ABD和△CAF中,
,
∴△ABD≌△CAF(ASA),
同理可证△CAF≌△BCE,
∴AD=BE=CF,BD=CE=AF,
∴DE=EF=FD,
∴△DEF为等边三角形;
(2)△ABD≌△CAF,△CAF≌△BCE,△ABD≌△BCE,
理由如下:
∵∠BAC=∠ACB=∠CBA,
∴△ABC为等边三角形,
∴AB=BC=AC,
∵∠1=∠2=∠3,
∴∠ABD=∠CAF=∠BCE,
在△ABD和△CAF中,
,
∴△ABD≌△CAF(ASA),
同理可证△CAF≌△BCE.
∴△ABC为等边三角形,
∴AB=BC=AC,
∵∠1=∠2=∠3,
∴∠ABD=∠CAF=∠BCE,
在△ABD和△CAF中,
|
∴△ABD≌△CAF(ASA),
同理可证△CAF≌△BCE,
∴AD=BE=CF,BD=CE=AF,
∴DE=EF=FD,
∴△DEF为等边三角形;
(2)△ABD≌△CAF,△CAF≌△BCE,△ABD≌△BCE,
理由如下:
∵∠BAC=∠ACB=∠CBA,
∴△ABC为等边三角形,
∴AB=BC=AC,
∵∠1=∠2=∠3,
∴∠ABD=∠CAF=∠BCE,
在△ABD和△CAF中,
|
∴△ABD≌△CAF(ASA),
同理可证△CAF≌△BCE.
点评:本题主要考查全等三角形的判定和性质及等边三角形的性质和判定,由条件得到∠ABD=∠CAF=∠BCE是解题的关键.

练习册系列答案
相关题目
下列各式运算正确的是( )
| A、a2+a3=a5 |
| B、a2•a3=a5 |
| C、(ab2)3=ab6 |
| D、a10÷a2=a5 |
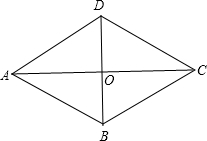 如图,菱形ABCD的周长为2p,对角线AC、BD交于O,AC+BD=q,求菱形ABCD的面积.(提示:利用两数和的平方公式(a+b)2=a2+2ab+b2与勾股定理)
如图,菱形ABCD的周长为2p,对角线AC、BD交于O,AC+BD=q,求菱形ABCD的面积.(提示:利用两数和的平方公式(a+b)2=a2+2ab+b2与勾股定理)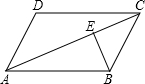 如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为
如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为 如图,在四边形ABCD中,已知AD∥BC,∠1=∠2,试说明∠3+∠4=180°.
如图,在四边形ABCD中,已知AD∥BC,∠1=∠2,试说明∠3+∠4=180°. 如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC.
如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC.