题目内容
1. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.(1)求证:点D在AB的中垂线上;
(2)如果△ACD的面积为1,求△ADB的面积.
分析 (1)利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
(2)利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比进而求出答案.
解答 (1)证明:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
根据作图方法可知,AD是∠CAB的角平分线,
∴∠1=∠B=30°,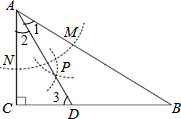
∴AD=BD,
∴点D在AB的中垂线上.
(2)解:∵如图,在直角△ACD中,∠2=30°,
∴CD=$\frac{1}{2}$AD,
∴BC=CD+BD=$\frac{1}{2}$AD+AD=$\frac{3}{2}$AD,S△DAC=$\frac{1}{2}$AC•CD=$\frac{1}{4}$AC•AD.
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AC•$\frac{3}{2}$AD=$\frac{3}{4}$AC•AD,
∴S△DAC:S△ABC=$\frac{1}{4}$AC•AD:$\frac{3}{4}$AC•AD=1:3,
∴S△DAC:S△ABD=1:2,
∵△ACD的面积为1,
∴△ADB的面积为:2.
点评 本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时,需要熟悉等腰三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.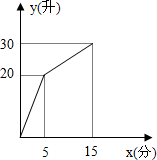 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )| A. | 22 | B. | 25 | C. | 27 | D. | 28 |
6. 如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
 如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )
如图,AB∥CD,BE交CD于点F,若∠B=50°,则∠DFE的度数为( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
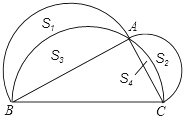 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π. 把下面四个图形拼成一个大长方形,并据此写出一个多项式的因式分解x2+3x+2=(x+2)(x+1).
把下面四个图形拼成一个大长方形,并据此写出一个多项式的因式分解x2+3x+2=(x+2)(x+1). 三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.
三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.