题目内容
用配方法解方程3x2-6x+1=0,则方程可变形为( )
A、(x-3)2=
| ||
B、3(x-1)2=
| ||
C、(x-1)2=
| ||
| D、(3x-1)2=1 |
考点:解一元二次方程-配方法
专题:计算题
分析:方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,变形即可得到结果.
解答:解:方程变形得:x2-2x=-
,
配方得:x2-2x+1=
,即(x-1)2=
,
故选C.
| 1 |
| 3 |
配方得:x2-2x+1=
| 2 |
| 3 |
| 2 |
| 3 |
故选C.
点评:此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
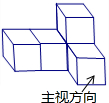 5个大小相同的正方体搭成的几何体如图,则下列说法中正确的是( )
5个大小相同的正方体搭成的几何体如图,则下列说法中正确的是( )| A、主视图的面积最小 |
| B、左视图的面积最小 |
| C、俯视图的面积最小 |
| D、三个视图面积一样大 |
| 1 |
| 2014 |
| A、2014 | ||
| B、-2014 | ||
C、-
| ||
D、
|
 如图,在Rt△ABC中,∠C=90°,AB=26cm,sinA=
如图,在Rt△ABC中,∠C=90°,AB=26cm,sinA= 如图,P是反比例函数y=
如图,P是反比例函数y= 如图,点A在第一象限,B(6,0),AC⊥OB,垂足为点C,双曲线y=
如图,点A在第一象限,B(6,0),AC⊥OB,垂足为点C,双曲线y=