题目内容
“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现舟山人追梦的风采,某校开展了“梦想中国,逐梦舟山”为主题的摄影大赛,要求参赛学生每人交一件作品,先将参赛的50件作品的成绩(单位:分)进行统计如下:
请根据上表提供的信息,解答下列问题:
(1)求表中的x、y的值;
(2)将本次参赛作品获得A等级的学生用A1,A2…表示,现该校决定从本次参赛作品中获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
| 等级 | 成绩(用S表示) | 频数 | 频率 |
| A | 90≤S≤100 | x | 0.06 |
| B | 80≤S<90 | 35 | y |
| C | S<80 | 12 | 0.24 |
| 合计 | / | 50 | 1 |
(1)求表中的x、y的值;
(2)将本次参赛作品获得A等级的学生用A1,A2…表示,现该校决定从本次参赛作品中获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
考点:列表法与树状图法
专题:
分析:(1)用50减去B等级与C等级的学生人数,即可求出A等级的学生人数x的值,用35除以50即可得出B等级的频率即y的值;
(2)由(1)可知获得A等级的学生有4人,用A1,A2,A3,A4表示,画出树状图,通过图确定恰好抽到学生A1和A2的概率.
(2)由(1)可知获得A等级的学生有4人,用A1,A2,A3,A4表示,画出树状图,通过图确定恰好抽到学生A1和A2的概率.
解答:解:(1)∵x+35+12=50,∴x=3,或x=50×0.06=3;
y=1-0.06-0.24=0.7;
(2)依题得获得A等级的学生有3人,用A1,A2,A3,表示,画树状图如下:

由上图可知共有6种结果,且每一种结果可能性都相同,其中抽到学生A1和A2的有两种结果,
所以从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,恰好抽到学生A1和A2的概率为:P=
.
y=1-0.06-0.24=0.7;
(2)依题得获得A等级的学生有3人,用A1,A2,A3,表示,画树状图如下:

由上图可知共有6种结果,且每一种结果可能性都相同,其中抽到学生A1和A2的有两种结果,
所以从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,恰好抽到学生A1和A2的概率为:P=
| 1 |
| 3 |
点评:本题考查读频数(率)分布表的能力和利用图表获取信息的能力.利用统计图表获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.用到的知识点为:各小组频数之和等于数据总数;各小组频率之和等于1;频率=频数÷数据总数;概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
用配方法解方程3x2-6x+1=0,则方程可变形为( )
A、(x-3)2=
| ||
B、3(x-1)2=
| ||
C、(x-1)2=
| ||
| D、(3x-1)2=1 |

 如图,正方形ABCD中,BE=CF.
如图,正方形ABCD中,BE=CF.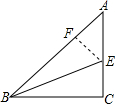 如图,Rt△ABC,AC=BC,将Rt△ABC沿过B的直线折叠,使点C落在AB边上点F处,折痕为BE,这样可以求出22.5°的正切值是
如图,Rt△ABC,AC=BC,将Rt△ABC沿过B的直线折叠,使点C落在AB边上点F处,折痕为BE,这样可以求出22.5°的正切值是