题目内容
13. 已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )
已知平面直角坐标系中,⊙M在第一象限内,点M的坐标为(a+1,a)(其中a>1),⊙M的半径为1,动点P在坐标轴上,过点P作⊙M的切线,则最短的切线长为( )| A. | a-1 | B. | a | C. | $\sqrt{{a}^{2}-1}$ | D. | $\sqrt{{a}^{2}+2a}$ |
分析 设切点为Q,连接MQ,如图,利用切线的性质得到∠PQM=90°,利用勾股定理得到PQ=$\sqrt{P{M}^{2}-1}$,由于M到x轴的距离为a,到y轴的距离为a+1,所以PM的最小值为a,于是得到PQ的最小值为$\sqrt{{a}^{2}-1}$.
解答 解:设切点为Q,连接MQ,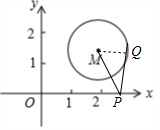 如图,
如图,
∵PQ为切线,
∴MQ⊥PQ,
∴∠PQM=90°,
∴PQ=$\sqrt{P{M}^{2}-M{Q}^{2}}$=$\sqrt{P{M}^{2}-1}$,
当PM最小时,PQ的值最小,
而M到x轴的距离为a,到y轴的距离为a+1,
∴PM的最小值为a,
∴PQ的最小值为$\sqrt{{a}^{2}-1}$.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了坐标与图形性质.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
3.若关于x的一元二次方程ax2-bx+4=0的解是x=2,则2017+2a-b=( )
| A. | 2015 | B. | 2017 | C. | 2019 | D. | 2020 |
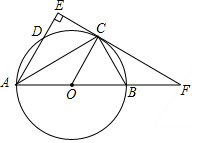 如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.
如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.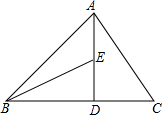 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.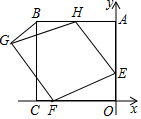 如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.