题目内容
在△ABC中,锐角A、B满足|sinA-
|+[cos(B-15°)-
]2=0,则△ABC是( )
| ||
| 2 |
| ||
| 2 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
考点:特殊角的三角函数值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据非负数的性质求出sinA和cos(B-15°)的值,然后求出∠A和∠B的度数,即可判断△ABC的形状.
解答:解:∵|sinA-
|+[cos(B-15°)-
]2=0,
∴sinA=
,cos(B-15°)=
,
则∠A=45°,∠B-15°=30°,
∴∠B=45°,∠C=90°,
故△ABC为等腰直角三角形.
故选C.
| ||
| 2 |
| ||
| 2 |
∴sinA=
| ||
| 2 |
| ||
| 2 |
则∠A=45°,∠B-15°=30°,
∴∠B=45°,∠C=90°,
故△ABC为等腰直角三角形.
故选C.
点评:本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
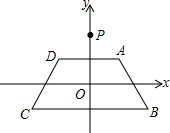 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )| A、(2010,2) |
| B、(2012,-2 ) |
| C、(0,2) |
| D、(2010,-2 ) |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A、a>0 |
| B、当x≥1时,y随x的增大而增大 |
| C、c<0 |
| D、当-1<x<3时,y>0 |
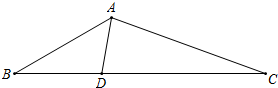 如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°.
如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°. 如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=
如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=
 如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是
如图,BD是∠ABC的平分线,DF⊥BC于点F,S△ABC=36cm2,BC=18cm,AB=12cm,则DF的长是