题目内容
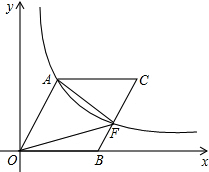 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=| 4 |
| 5 |
| k |
| x |
(1)若OA=5,求反比例函数的解析式;
(2)若点F为BC的中点,OA=10,求点C的坐标.
考点:平行四边形的性质,反比例函数图象上点的坐标特征,待定系数法求反比例函数解析式
专题:
分析:(1)先过点A作AH⊥OB,根据sin∠AOB=,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
(2)利用OA=10,过点F作FM⊥x轴于M,根据sin∠AOB=
,得出AH=8,OH=6,求出k的值,进而得出F点坐标,进而得出C点坐标.
(2)利用OA=10,过点F作FM⊥x轴于M,根据sin∠AOB=
| 4 |
| 5 |
解答:解:(1)过点A作AH⊥OB于H,
∵sin∠AOB=
,OA=5,
∴AH=4,OH=3,
∴A点坐标为(3,4),
∵反比例函数y=
(k>0)过(3,4)
可得:k=12,
∴反比例函数解析式:y=
(x>0);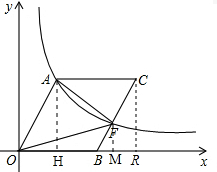
(2)过点F作FM⊥x轴于M,过点C作CR⊥x轴于点R,
∵四边形AOBC是平行四边形,
∴AO∥BC,AO=CB=10,
∴∠AOB=∠CBM,
∵sin∠AOB=
,
∴sin∠CBM=
,
则AH=8,OH=6,
∵点F为BC的中点,
∴BF=5,
∴FM=4,
∴BM=3,
∵F在反比例函数图象上,
∴
OM×FM=24,
解得:OM=12,
由题意可得:FM=
CR,BM=
BR,
则BM=MR=3,
故C(15,10).
∵sin∠AOB=
| 4 |
| 5 |
∴AH=4,OH=3,
∴A点坐标为(3,4),
∵反比例函数y=
| k |
| x |
可得:k=12,
∴反比例函数解析式:y=
| 12 |
| x |

(2)过点F作FM⊥x轴于M,过点C作CR⊥x轴于点R,
∵四边形AOBC是平行四边形,
∴AO∥BC,AO=CB=10,
∴∠AOB=∠CBM,
∵sin∠AOB=
| 4 |
| 5 |
∴sin∠CBM=
| 4 |
| 5 |
则AH=8,OH=6,
∵点F为BC的中点,
∴BF=5,
∴FM=4,
∴BM=3,
∵F在反比例函数图象上,
∴
| 1 |
| 2 |
解得:OM=12,
由题意可得:FM=
| 1 |
| 2 |
| 1 |
| 2 |
则BM=MR=3,
故C(15,10).
点评:此题主要考查了平行四边形的性质以及反比例函数的性质等知识,得出A点坐标是解题关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
观察下列命题:①邻补角互补; ②对顶角相等; ③同旁内角互补; ④两点之间线段最短,其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知点A(-2,5),点B与点A关于原点O对称,则点B的坐标是( )
| A、(-2,5) |
| B、(-2,-5) |
| C、(2,5) |
| D、(2,-5) |
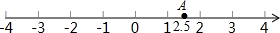 如图,在数轴上画出表示3.5的相反数的点B,再把点A向左移动1.5个单位,得到点C.
如图,在数轴上画出表示3.5的相反数的点B,再把点A向左移动1.5个单位,得到点C.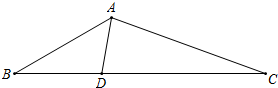 如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°.
如图,在△ABC中,点D在BC上,AC=CD,∠B=30°,∠ADB=100°. 如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=
如图所示,PA切⊙O于A,OP交⊙O于B,且PB=1,PA=