题目内容
2.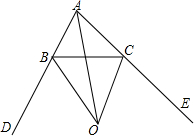 如图,△ABC的内角∠BAC的平分线和外角∠DBC的平分线交于点O,连接CO,求证:CO平分△ABC的外角∠BCE.
如图,△ABC的内角∠BAC的平分线和外角∠DBC的平分线交于点O,连接CO,求证:CO平分△ABC的外角∠BCE.
分析 作OF⊥AD于F,OG⊥BC于G,OH⊥AE于H,根据角平分线的性质得到OF=OG,OF=OH,得到OG=OH,根据角平分线的判定定理证明结论.
解答 证明: 作OF⊥AD于F,OG⊥BC于G,OH⊥AE于H,
作OF⊥AD于F,OG⊥BC于G,OH⊥AE于H,
∵OB平分∠DBC,OF⊥AD,OG⊥BC,
∴OF=OG,
∵OA平分∠BAC,OF⊥AD,OH⊥AE,
∴OF=OH,
∴OG=OH,OG⊥BC,OH⊥AE,
∴CO平分△ABC的外角∠BCE.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
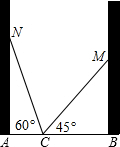 如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度.
如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度. 如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,
如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,