题目内容
20. 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
分析 求出∠DCA的度数,再判断出BC=CD,据此即可判断出△BCD是等边三角形.过点B作BE⊥AD,垂足为E,求出∠DAC的度数,利用三角函数求出AB的长,从而得到AB+BC+CD的长.
解答 解:由题意可知∠DCA=180°-75°-45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
过点B作BE⊥AD,垂足为E,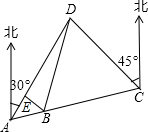 如图所示:
如图所示:
由题意可知∠DAC=75°-30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60° BD=BC=CD=20km,
∴∠ADB=∠DBC-∠DAC=15°,
∴BE=sin15°BD≈0.25×20≈5m,
∴AB=$\frac{BE}{sin45°}$=$\frac{5}{\frac{\sqrt{2}}{2}}$≈7m,
∴AB+BC+CD≈7+20+20≈47m.
答:从A地跑到D地的路程约为47m.
点评 本题考查了解直角三角形的应用--方向角问题;通过解直角三角形求出AB是解决问题的关键.

练习册系列答案
相关题目
11.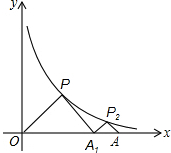 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
 如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )
如图,△POA1、△P2A1A都是等腰直角三角形,直角顶点P、P2在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A都在x轴上,则点A的坐标是( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (2,0) | D. | (2$\sqrt{2}$,0) |
15.已知抛物线y=2(x-1)2上的两点A(x1,y1)和B(x2,y2),如果x1<x2<0,那么下列结论一定成立的是( )
| A. | y1<y2<0 | B. | 0<y1<y2 | C. | 0<y2<y1 | D. | y2<y1<0 |
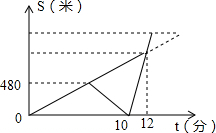 小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.
小明和哥哥以每分钟80米的速度从家出发步行去爷爷家.在途中,哥哥发现忘记带给爷爷买的礼物,于是小明继续前行,哥哥以每分钟120米的速度沿原路跑回家,然后乘出租车赶往爷爷家,途中追上小明后,带上他一同乘车到爷爷家,结果到爷爷家的时间比预计步行的时间早了3分钟(其中回家取东西、上下车时间忽略不计).如图反映了小明和哥哥离家距离与时间之间的关系.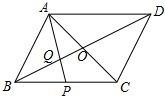 如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$. 如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)
如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$) 如图,一喷泉喷出的水流的形状由抛物线OAB逐渐变化到抛物线OCD,再由抛物线OCD逐渐变化到抛物线OAB,如此反复,在如图所示的坐标系中,这些抛物线都满足关系式y=-(x-k)2+h.
如图,一喷泉喷出的水流的形状由抛物线OAB逐渐变化到抛物线OCD,再由抛物线OCD逐渐变化到抛物线OAB,如此反复,在如图所示的坐标系中,这些抛物线都满足关系式y=-(x-k)2+h.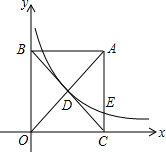 如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x.
如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x. 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )