题目内容
12. 如图,一喷泉喷出的水流的形状由抛物线OAB逐渐变化到抛物线OCD,再由抛物线OCD逐渐变化到抛物线OAB,如此反复,在如图所示的坐标系中,这些抛物线都满足关系式y=-(x-k)2+h.
如图,一喷泉喷出的水流的形状由抛物线OAB逐渐变化到抛物线OCD,再由抛物线OCD逐渐变化到抛物线OAB,如此反复,在如图所示的坐标系中,这些抛物线都满足关系式y=-(x-k)2+h.(1)求当k=2时,抛物线的解析式;
(2)若喷泉喷出的水流为抛物线OCD,这时喷出水流的最大高度为4m,求此时水流喷出的最远距离OD是多少?
(3)若OB=2,此时抛物线OAB水流的最大高度是多少?
分析 (1)将k=2,原点(0,0)代入y=-(x-k)2+h求得h的值即可求解;
(2)由(1)知当喷出水流的最大高度为4m时解析式为y=-(x-2)2+4,令y=0求出x即可;
(3)由OB=2得对称轴k=1,即抛物线解析式为y=-(x-1)2+h,在将原点(0,0)代入求得h可得.
解答 解:(1)当k=2时,y=-(x-2)2+h,
将原点(0,0)代入得:-4+h=0,
解得:h=4,
故抛物线解析式为:y=-(x-2)2+4;
(2)由(1)知当喷出水流的最大高度为4m时,抛物线解析式为:y=-(x-2)2+4,
当y=0时,-(x-2)2+4=0,
解得:x1=0(舍),x2=4,
故此时水流喷出的最远距离OD是4米;
(3)当OB=2时,抛物线OAB的对称轴为x=1,
∴此时抛物线解析式为y=-(x-1)2+h,
将点(0,0)代入得:-1+h=0,解得:h=1,
∴抛物线OAB的解析式为y=-(x-1)2+1,即抛物线OAB水流的最大高度是1米.
点评 本题是二次函数的实际应用,掌握抛物线顶点式y=-(x-k)2+h中h、k的实际意义是解题的关键.

练习册系列答案
相关题目
2.一个盒子中装有2个白球、5个红球,从这个盒子中随机摸出一个球,是红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{2}$ |
7.我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,25,22,25,26,27,则这组数据的中位数与众数分别是( )
| A. | 25,25 | B. | 25,22 | C. | 20,22 | D. | 22,24 |
17.下列事件中,属于随机事件的是( )
| A. | 测量某天的最高气温是100℃ | |
| B. | 度量四边形的内角和,结果是360° | |
| C. | 掷一枚骰子,向上一面的数字是2 | |
| D. | 袋中装有5只黑球,从中摸出一个是黑球 |
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)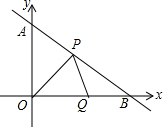 综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.