题目内容
8.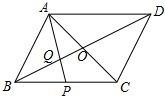 如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$.
分析 连接OP,只要证明OP是△ACB的中位线,利用三角形中位线性质即可解决问题.
解答 解:连接OP,
∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵PC=PB,
∴OP∥AB,OP=$\frac{1}{2}$AB,
∴$\frac{OP}{AB}$=$\frac{OQ}{QB}$=$\frac{1}{2}$,
∴$\frac{OQ}{OB}$=$\frac{1}{3}$,
故答案为$\frac{1}{3}$.
点评 本题考查相似三角形的性质、平行四边形的性质、三角形中位线定理等知识,解题的关键是三角形中位线定理的应用,属于中考常考题型.

练习册系列答案
相关题目
19.下列各式中,不论字母取何值时分式都有意义的是( )
| A. | $\frac{1}{2x+1}$ | B. | $\frac{1}{2x-1}$ | C. | $\frac{1-3x}{{x}^{2}}$ | D. | $\frac{5x+3}{2{x}^{2}+1}$ |
16.a与$\frac{1}{3}$互为相反数,则a的倒数是( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
13.不等式1-2x>3的解集是( )
| A. | x>1 | B. | x>-1 | C. | x<1 | D. | x<-1 |
17.下列事件中,属于随机事件的是( )
| A. | 测量某天的最高气温是100℃ | |
| B. | 度量四边形的内角和,结果是360° | |
| C. | 掷一枚骰子,向上一面的数字是2 | |
| D. | 袋中装有5只黑球,从中摸出一个是黑球 |
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)