题目内容
14．关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=2m+1}\\{x+2y=3}\end{array}\right.$的解满足不等式x-y＞4，则m的取值范围是m＞3．分析 先把两式相减求出x-y的值，再代入x-y＞4中得到关于m的不等式，求出m的取值范围即可．
解答 解：$\left\{\begin{array}{l}{2x+y=2m+1①}\\{x+2y=3②}\end{array}\right.$，
①-②得，x-y=2m-2，
∵x-y＞4，
∴2m-2＞4，
解得m＞3．
故答案为m＞3．
点评 本题考查的是解二元一次方程组及解二元一次不等式组，解答此题的关键是把m当作已知条件表示出x、y的值，再得到关于m的不等式．
练习册系列答案
相关题目
4．下列图形既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
5．已知等边三角形的边长为4，则它的高为（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 8$\sqrt{3}$ |
9．
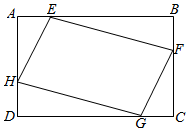如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（ ）
如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（ ）| A． | 5$\sqrt{5}$ | B． | 10$\sqrt{5}$ | C． | 10$\sqrt{3}$ | D． | 15$\sqrt{3}$ |
19．下列各图中，∠1和∠2是对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．下列图形是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
