题目内容
14.解方程或不等式组:(1)$\frac{1}{x-1}-\frac{2x}{{{x^2}-1}}=1$
(2)$\left\{\begin{array}{l}\frac{x-3}{2}+3>x+1\\ 1-3(x-1)≤8-x\end{array}\right.$.
分析 (1)先把方程两边乘以(x+1)(x-1),原方程可化为x2+x-2=0,然后解此一元二次方程,再进行检验确定原方程的解;
(2)分别解两个不等式得到x<1和x≥-2,然后根据大小小大中间找确定不等式组的解集.
解答 解:(1)去分母得x+1-2x=x2-1,
整理得x2+x-2=0,解得x1=-2,x2=1,
经检验x=1是原方程的增根,
所以原方程的解为x=-2;
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3>x+1①}\\{1-3(x-1)≤8-x②}\end{array}\right.$,
解①得x<1,
解②得x≥-2,
所以不等式组的解集为-2≤x<1.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.也考查了解分式方程.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
5.下面四个图形中,线段BD是△ABC的高的是( )
| A. |  | B. |  | C. |  | D. |  |
4.已知抛物线y=ax2+2ax+4(0<a<3),A(x1,y1)B(x2,y2)是抛物线上两点,若x1>x2,且x1+x2=1-a,则( )
| A. | y1<y2 | B. | y1=y2 | ||
| C. | y1>y2 | D. | y1与y2的大小不能确定 |
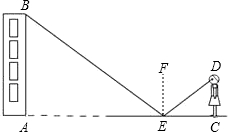 小强用这样的方法来测量学校教学楼的高度:如图,在地面上放一面镜子(镜子高度忽略不计),他刚好能从镜子中看到教学楼的顶端B,他请同学协助量了镜子与教学楼的距离EA=21米,以及他与镜子的距离CE=2.5米,已知他的眼睛距离地面的高度DC=1.6米,请你帮助小强计算出教学楼的高度.(根据光的反射定律:反射角等于入射角)
小强用这样的方法来测量学校教学楼的高度:如图,在地面上放一面镜子(镜子高度忽略不计),他刚好能从镜子中看到教学楼的顶端B,他请同学协助量了镜子与教学楼的距离EA=21米,以及他与镜子的距离CE=2.5米,已知他的眼睛距离地面的高度DC=1.6米,请你帮助小强计算出教学楼的高度.(根据光的反射定律:反射角等于入射角)