题目内容
19.计算(1)$\sqrt{4}$+(π-3.14)0-|-5|+(-1)2012+($\frac{1}{3}$)-2
(2)6x3y2÷(-$\frac{y}{x}$)2•$\frac{x}{y^2}$÷x2
(3)$\frac{m-15}{m2-9}$-$\frac{2}{3-m}$
(4)$\frac{x^2}{x-1}$-x-1.
分析 (1)根据零指数幂与负整数指数幂的意义得到原式=2+1-5+1+9,然后进行加减运算;
(2)先进行乘方运算,再把除法运算化为乘法运算,然后约分即可;
(3)先进行通分得到原式=$\frac{m-15+2(m+3)}{(m+3)(m-3)}$,然后把分子合并后因式分解,再约分即可;
(4)先进行通分,然后进行同分母的减法运算即可.
解答 解:(1)原式=2+1-5+1+9
=8;
(2)原式=6x3y2÷$\frac{{y}^{2}}{{x}^{2}}$•$\frac{x}{y^2}$÷x2
=6x3y2•$\frac{{x}^{2}}{{y}^{2}}$•$\frac{x}{y^2}$•$\frac{1}{{x}^{2}}$
=$\frac{6{x}^{3}}{{y}^{2}}$;
(3)原式=$\frac{m-15}{(m+3)(m-3)}$+$\frac{2}{m-3}$
=$\frac{m-15+2(m+3)}{(m+3)(m-3)}$
=$\frac{3(m-3)}{(m+3)(m-3)}$
=$\frac{3}{m+3}$;
(4)原式=$\frac{{x}^{2}}{x-1}$-$\frac{(x+1)(x-1)}{x-1}$
=$\frac{{x}^{2}-({x}^{2}-1)}{x-1}$
=$\frac{1}{x-1}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了零指数幂与负整数指数幂.

练习册系列答案
相关题目
7.一元二次方程x2-4=0的根为( )
| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x=4 |
11.下面各条件中,能判定四边形是平行四边形的是( )
| A. | 对角线互相垂直 | B. | 对角线互相平分 | C. | 一组对角相等 | D. | 一组对边相等 |
9.25的平方根是( )
| A. | 5 | B. | -5 | C. | ±$\sqrt{5}$ | D. | ±5 |
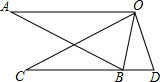 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=30°.
如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=30°.