题目内容
10.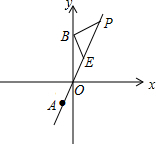 如图,点A(-1,-2)为正比例函数y=kx的图象上一点,B(0,4).
如图,点A(-1,-2)为正比例函数y=kx的图象上一点,B(0,4).(1)求k的值;
(2)点P为第一象限的正比例函数图象上一点,BE⊥BP交OP于E,若BP=BE.求点P的坐标.
分析 (1)根据点A的坐标利用待定系数法即可求出正比例函数解析式;
(2)过点B作BC⊥直线AP于点C,过点P作PD⊥y轴于点D,由点B的坐标结合勾股定理即可得出BC、OC的长度,再根据等腰直角三角形的性质即可得出CP的长度,进而可得出OP的长度,根据正比例函数图象上点的坐标特征以及勾股定理即可求出OD、DP的长度,从而得出点P的坐标.
解答 解:(1)将点A(-1,-2)代入y=kx,
-2=-1k,
解得:k=2.
(2)过点B作BC⊥直线AP于点C,过点P作PD⊥y轴于点D,如图所示.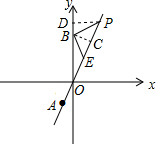
∵正比例函数解析式为y=2x,BC⊥OC,
∴OC=2BC,OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{5}$BC.
∵点B(0,4),
∴OB=4,BC=$\frac{4\sqrt{5}}{5}$,OC=$\frac{8\sqrt{5}}{5}$.
∵BE⊥BP,BP=BE,
∴△BEP为等腰直角三角形,
∴CP=BC=$\frac{4\sqrt{5}}{5}$,OP=OC+CP=$\frac{12\sqrt{5}}{5}$.
∵DP⊥y轴,
∴OD=2DP,OP=$\sqrt{O{D}^{2}+D{P}^{2}}$=$\sqrt{5}$DP,
∴DP=$\frac{12}{5}$,OD=$\frac{24}{5}$.
∴点P的坐标为($\frac{12}{5}$,$\frac{24}{5}$).
点评 本题考查了一次函数图象上点的坐标特征、待定系数法求正比例函数解析式以及勾股定理,解题的关键是:(1)根据点的坐标利用待定系数法求出正比例函数解析式;(2)根据一次函数图象上点的坐标特征结合勾股定理求出OD、DP的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.据新华网报道,在新一期全球超级计算机500强榜单中,中国“神威•太湖之光”继续以每秒930 000 000亿次的浮点运算速度领跑,数930 000 000用科学记数法可表示为( )
| A. | 0.93×109 | B. | 9.3×108 | C. | 9.3×109 | D. | 93×107 |
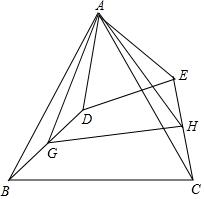 如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.
如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.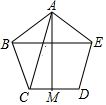 如图所示,在正五边形ABCDE中,M是CD的中点,连接AC,BE,AM.求证:
如图所示,在正五边形ABCDE中,M是CD的中点,连接AC,BE,AM.求证: