题目内容
4. 如图,△ABC中,AB=AC,∠A=45°,AC的垂直平分线分别交AB、AC于D、E,若CD=1,则BD等于( )
如图,△ABC中,AB=AC,∠A=45°,AC的垂直平分线分别交AB、AC于D、E,若CD=1,则BD等于( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
分析 证明△ADC为等腰直角三角形,求得AC,从而得到AB,再根据线段的和差关系即可求解.
解答 解:∵AC的垂直平分线分别交AB、AC于D、E,
∴AD=CD,∠ACD=∠A=45°,
∴△ADC为等腰直角三角形,
∵CD=1,
∴AC=$\sqrt{2}$,
∴AB=$\sqrt{2}$,
∴BD=AB-AD=$\sqrt{2}$-1.
故选:D.
点评 此题考查了线段垂直平分线的性质,等腰三角形的性质,等腰直角三角形的判定和性质,此题的关键是先证明△ADC为等腰直角三角形.

练习册系列答案
相关题目
12.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
| A. | 24 cm和12 cm | B. | 16 cm和22 cm | C. | 20 cm和16 cm | D. | 22 cm和16 cm |
19.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 矩形的对角线相等 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 对角线相等的四边形是矩形 |
9.下列命题中,是真命题的是( )
| A. | 两个锐角的和是锐角 | |
| B. | 邻补角是互补的角 | |
| C. | 同旁内角互补 | |
| D. | 两条直线被第三条直线所截,内错角相等 |
3.已知青椒每斤3元,西红柿每斤2元,小张妈妈以每斤2.5元混合买了a斤青椒和b斤西红柿,结果小张发现妈妈亏钱了,原因是( )
| A. | a<b | B. | a>b | C. | a=b | D. | 与a,b大小无关 |
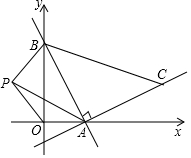 如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.
如图,一次函数y=-2x+4与x轴,y轴分别交于A,B,以线段AB为直角边在第一象限内作Rr△ABC,使AB=AC.