题目内容
10. 如图,已知,在△ABC中,AB=AC,AD是∠BAC的平分线交BC于点D,E、F分别为AB、AC的中点.求证:四边形AEDF是菱形.
如图,已知,在△ABC中,AB=AC,AD是∠BAC的平分线交BC于点D,E、F分别为AB、AC的中点.求证:四边形AEDF是菱形.
分析 根据等腰三角形的性质可得BD=CD,AD⊥BC,再根据三角形的中位线定理可得ED∥AC,DF∥AB,进而可得四边形AEDF是平行四边形,再根据直角三角形斜边上的中线等于斜边的一半可得DE=DF,进而可得四边形AEDF是菱形.
解答 证明:∵AB=AC,AD是∠BAC的平分线交BC于点D,
∴BD=CD,
∵E、F分别为AB、AC的中点,
∴ED∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AB=AC,AD是∠BAC的平分线交BC于点D,
∴AD⊥BC,
∵E、F分别为AB、AC的中点,
∴DE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$AC,
∴DE=DF,
∴四边形AEDF是菱形.
点评 此题主要考查了菱形的判定,以及三角形中位线定理,直角三角形的性质,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
19.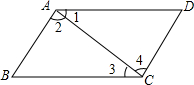 如图,下列判断错误的是( )
如图,下列判断错误的是( )
 如图,下列判断错误的是( )
如图,下列判断错误的是( )| A. | 如果∠2=∠4,那么AB∥CD | B. | 如果∠1=∠3,那么AB∥CD | ||
| C. | 如果∠BAD+∠D=180,那么AB∥CD | D. | 如果∠BAD+∠B=180,那么AD∥CD |
 (1)如图,工人师傅要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,使其圆心在线段AC上,且与AB、BC都相切.请你在图中画出这个半圆.(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).
(1)如图,工人师傅要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,使其圆心在线段AC上,且与AB、BC都相切.请你在图中画出这个半圆.(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).