题目内容
10.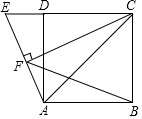 如图,在正方形ABCD中,点E在CD的延长线上,且CE=CA,连接AE,过点C作CF⊥AE于点F,连接BF.如果AB=4,则BF2的值为16+8$\sqrt{2}$.
如图,在正方形ABCD中,点E在CD的延长线上,且CE=CA,连接AE,过点C作CF⊥AE于点F,连接BF.如果AB=4,则BF2的值为16+8$\sqrt{2}$.
分析 连接DF,作FH⊥CE于H,首先证明△FDC≌△FAB,推出FC=FB,在Rt△CFH中,求出FH、CH即可解决问题.
解答 解:连接DF,作FH⊥CE于H.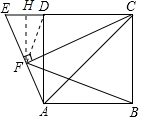
∵CE=CA,CF⊥EC,
∴EF=AF,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ADC=∠ADE=∠DAB=90°,
∴DF=AF,AC=CE=4$\sqrt{2}$,
∴∠FDA=∠FAD,
∴∠FDC=∠FAB,∵DC=AB,
∴△FDC≌△FAB,
∴FC=FB,
∴DE=CE-CD=4$\sqrt{2}$-4,
在Rt△FCH中,易知FH=2,CH=2$\sqrt{2}$+2,
∴CF2=FH2+CH2=16+8$\sqrt{2}$,
∴BF2=16+8$\sqrt{2}$,
故答案为16+8$\sqrt{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.如果直角三角形的边长为3,4,a,则a的值是( )
| A. | 5 | B. | 6 | C. | $\sqrt{7}$ | D. | 5或$\sqrt{7}$ |
19.A、B两店以同样价格出售一种商品,并推出不同的优惠方案;在A店累计购物超过100元后,超出100元的部分打9折;在B店累计购物超过50元后,超出50元的部分打9.5折,则顾客到两店购物花费一样时为( )
| A. | 累计购物不超过50元 | |
| B. | 累计购物超过50元而不超过100元 | |
| C. | 累计购物超过100元 | |
| D. | 累计购物不超过50元或刚好为150元 |
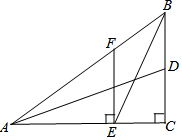 如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个
如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个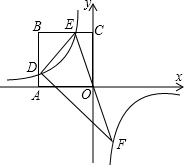 如图,在平面直角坐标系中,x轴上有一点A(a,0),其中a<0,以OA为边长作正方形ABCO,边AB与BC分别交双曲线y=$\frac{k}{x}$第二象限中的一支于点D、E,延长EO交双曲线的另一支于点F,连接DF.
如图,在平面直角坐标系中,x轴上有一点A(a,0),其中a<0,以OA为边长作正方形ABCO,边AB与BC分别交双曲线y=$\frac{k}{x}$第二象限中的一支于点D、E,延长EO交双曲线的另一支于点F,连接DF. 如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?
如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?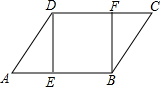 如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,