题目内容
16.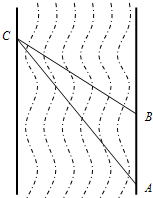 小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.
小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.(结果精确到0.1,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 要求CD的长,需要构造直角三角形,作CD⊥AB于点D,然后根据题目中的条件可以求得CD的长,本题得以解决.
解答 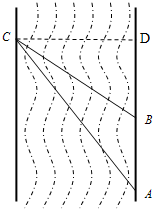 解:过点C作CD⊥AB,垂足为点D,如右图所示,
解:过点C作CD⊥AB,垂足为点D,如右图所示,
在Rt△CAD中,tan∠CAD=$\frac{CD}{AD}$,
∴AD=$\frac{CD}{tan∠CAD}$=$\frac{CD}{tan37°}$,
在Rt△CBD中,tan∠CBD=$\frac{CD}{BD}$,∠CBA=120°,
∴∠CBD=60°,
∴BD=$\frac{CD}{tan∠CBD}$=$\frac{CD}{tan60°}$,
∵AD-BD=AB,
∴$\frac{CD}{tan37°}$-$\frac{CD}{tan60°}$=31,
$\frac{CD}{0.75}$-$\frac{CD}{\sqrt{3}}$=31,
解得,CD≈41.0,
即这条河的宽度约为41.0米.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数进行解答.

练习册系列答案
相关题目
6.在平面直角坐标系中,在第四象限内有一点P,且点P到x轴的距离是4,到y轴的距离是5,则点P的坐标为( )
| A. | (4,-5) | B. | (4,5) | C. | (-5,-4) | D. | (5,-4) |
4.下列正多边形的地砖中,不能铺满地面的正多边形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
5.若用规格相同的正六边形地砖铺地板,则围绕在一个顶点处的地砖的块数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
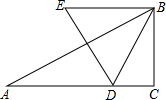 如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.
如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.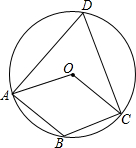 如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.
如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.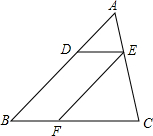 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.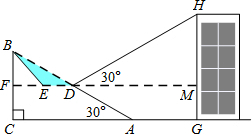 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).