题目内容
6.某公园计划砌一个形状如图(1)所示的喷水池.(1)有建议改为图(2)所示的形状,且外直径不变,只是担心原来准备好的材料不够,请你比较两种方案,哪一种需要的材料多(即比较哪个周长更长)?
(2)若将三个小圆改成n个小圆,结论是否成立?请说明.
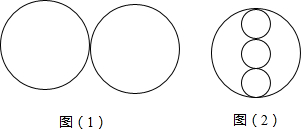
分析 (1)设大圆的半径为R,利用圆的周长公式得到图(1)中两个圆的周长为4πR;同样设图(2)三个小圆的半径分别为r1、r2、r3,则三个小圆的周长为2π(r1+r2+r3),由于r1+r2+r3=R,则三个小圆的周长=2πR,所以图(2)中所有圆的周长为4πR,于是可判断两种方案需要的材料一样多;
(2)设n个小圆的半径分别为r1、r2、…,rn,与(1)一样可得n个小圆的周长为2π(r1+r2+…+rn),而r1+r2+…+rn=R,则n个小圆的周长=2πR,所以所有圆的周长为4πR,于是可判断(1)中的结论仍然成立.
解答 解:(1)设大圆的半径为R,则图(1)中两个圆的周长=2•2πR=4πR,
设图(2)三个小圆的半径分别为r1、r2、r3,则三个小圆的周长=2πr1+2πr2+2πr3=2π(r1+r2+r3),
因为r1+r2+r3=R,
所以三个小圆的周长=2πR,
所以图(2)中所有圆的周长=2πR+2πR=4πR,
所以两种方案需要的材料一样多;
(2)将三个小圆改成n个小圆,结论成立.理由如下:
设n个小圆的半径分别为r1、r2、…,rn,则n个小圆的周长=2πr1+2πr2+…+2πrn=2π(r1+r2+…+rn),
因为r1+r2+…+rn=R,
所以n个小圆的周长=2πR,
所以所有圆的周长=2πR+2πR=4πR,
所以两种方案需要的材料一样多.
点评 本题考查了圆的认识:圆可以看做是所有到定点O的距离等于定长r的点的集合,掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
14.下列变形中正确的是( )
| A. | 9-x2+2xy-y2=9-(-x2-2xy+y2) | B. | 9-x2+2xy-y2=9-(x2-2xy-y2) | ||
| C. | 9-x2+2xy-y2=9-(x2-2xy+y2) | D. | 9-x2+2xy-y2=9+(x2-2xy+y2) |
11.根据下表,回答下列问题.
(1)278.89的平方根是多少?
(2)$\sqrt{259.21}$≈16.1.
(3)$\sqrt{280}$在表中哪两个相邻的数之间?为什么?
| x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(2)$\sqrt{259.21}$≈16.1.
(3)$\sqrt{280}$在表中哪两个相邻的数之间?为什么?
18.如图中,正确画出△ABC边AC上的高AE的是( )
| A. |  | B. |  | C. |  | D. |  |
16.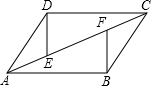 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有( )
如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有( )
 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有( )
如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
 为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系?
为扩大绿地面积,要把街心花园的一块长m米,宽a米,向两边分别加宽b米和c米.请你画出草图并用两种方法表示扩大后的绿地面积,思考这两种表示方法有何关系?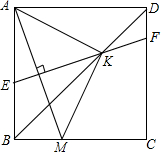 如图,正方形ABCD中,点M是边BC上一点(异于点B、C),AM的垂直平分线分别交AB、CD、BD于E、F、K,连AK、MK.
如图,正方形ABCD中,点M是边BC上一点(异于点B、C),AM的垂直平分线分别交AB、CD、BD于E、F、K,连AK、MK.