题目内容
5.如图,开口向下的抛物线y=ax2+bx+c交x轴于A(-1,0)、B(5,0)两点,交y轴于点C(0,5)(1)求抛物线的解析式;
(2)设抛物线的顶点为D,求△BCD的面积;
(3)在(2)的条件下,P、Q为线段BC上两点(P左Q右,且P、Q不与B、C重合),PQ=2$\sqrt{2}$,在第一象限的抛物线上是否存在这样的点R,使△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.
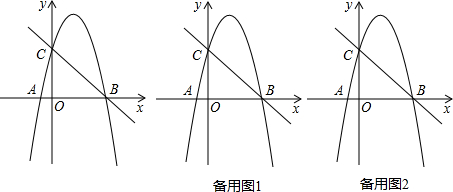
分析 (1)直接把点A(-1,0)、B(5,0),C(0,5)代入抛物线y=ax2+bx+c,利用待定系数法即可得出抛物线的解析式;
(2)作DE⊥AB于E,交对称轴于F,根据(1)求得的解析式得出顶点坐标,然后根据S△BCD=S△CDF+S△BDF即可求得;
(3)分三种情况:①以点P为直角顶点;②以点R为直角顶点;③以点Q为直角顶点;进行讨论可得使△PQR为等腰直角三角形时点R的坐标.
解答 解:(1)∵抛物线y=ax2+bx+c与x轴交于两点A(-1,0),B(5,0),C(0,5)
∴$\left\{\begin{array}{l}{a-b+c=0}\\{25a+5b+c=0}\\{c=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=5}\end{array}\right.$.
∴此抛物线的解析式为:y=-x2+4x+5;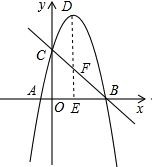
(2)由y=-x2+4x+5=-(x-2)2+9可知顶点D的坐标为(2,9),
作DE⊥AB于E,交对称轴于F,如图,
∴E(2,0),
∵B(5,0),C(0,5)
∴直线BC的解析式为y=-x+5,
把x=2代入得,y=3,
∴F(2,3),
∴DF=9-3=6,
S△BCD=S△CDF+S△BDF=$\frac{1}{2}$×6×2-$\frac{1}{2}$×6×(5-2)=$\frac{1}{2}$×6×5=15;
(3)分三种情况:
①以点P为直角顶点,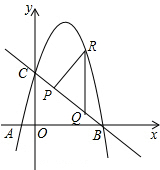
∵PQ=2$\sqrt{2}$,
∴RQ=$\sqrt{2}$PQ=4
∵C(0,5),B(5,0),
∴OC=OB=5,
∴∠OCB=∠OBC=45°,
∵∠RQP=45°
∴RQ∥OC
可求得直线BC的解析式为y=-x+5,
设R(m,-m2+4m+5),则Q(m,-m+5)
则RQ=(-m2+4m+5)-(-m+5)=4
解得m1=4,m2=1,
∵点Q在点P右侧,
∴m=4,
∴R(4,5);
②以点R为直角顶点,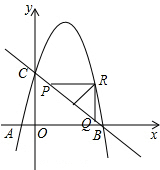
∵PQ=2$\sqrt{2}$,
∴RQ=$\frac{\sqrt{2}}{2}$PQ=2
设R(m,-m2+4m+5)则Q(m,-m+5),则RQ=(-m2+4m+5)-(-m+5)=2,
解得m1=$\frac{5+\sqrt{17}}{2}$,m2=$\frac{5-\sqrt{17}}{2}$,
∵点Q在点P右侧,
∴m=$\frac{5+\sqrt{17}}{2}$,
∴R($\frac{5+\sqrt{17}}{2}$,$\frac{9-\sqrt{17}}{2}$);
③以点Q为直角顶点,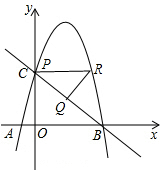
∵PQ=2$\sqrt{2}$∴PR=$\sqrt{2}$PQ=4
∵C(0,5),B(5,0)
∴OC=OB=5
∴∠OCB=∠OBC=45°
∵∠RPQ=45°,
∴PR∥OB
设R(m,-m2+4m+5),则P(m-4,-m2+4m+5),
把P(m-4,-m2+4m+5)代入y=-x+5,得-(m-4)+5=-m2+4m+5
解得m1=4,m2=1,
此时点P(0,5)
因为点P在线段BC上运动,且不与B、C重合,所以不存在以Q为直角顶点的情况.
综上所述:当 R(4,5)或(($\frac{5+\sqrt{17}}{2}$,$\frac{9-\sqrt{17}}{2}$)时,△PQR为等腰直角三角形.
点评 考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,顶点坐标,面积计算,等腰直角三角形的判定与性质,以及分类思想的应用,综合性较强,有一定的难度.

 阅读快车系列答案
阅读快车系列答案| A. | 13 | B. | 11 | C. | 7 | D. | 5 |
 有意义,则x的取值范围是 .
有意义,则x的取值范围是 .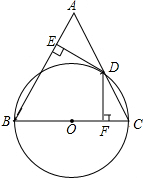 如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.