题目内容
1. 请根据如图所示的已知条件,求出抛物线解析式,并写出顶点坐标.
请根据如图所示的已知条件,求出抛物线解析式,并写出顶点坐标.
分析 设交点式y=a(x+1)(x-3),再把(0,2)代入求出a即可得到抛物线解析式,然后把一般式化为顶点式即可得到抛物线的顶点坐标.
解答 解:抛物线经过点(-1,0),(3,0),(0,2),
设抛物线解析式为y=a(x+1)(x-3),
把(0,2)代入得a•1•(-3)=2,解得a=-$\frac{2}{3}$,
所以抛物线解析式为y=-$\frac{2}{3}$(x+1)(x-3),即y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2,
因为y=-$\frac{2}{3}$(x-1)2+$\frac{8}{3}$,
所以抛物线的顶点坐标为(1,$\frac{8}{3}$).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
9.请你估计一下$\frac{({2}^{2}-1)({3}^{2}-1)({4}^{2}-1)…(201{5}^{2}-1)(201{6}^{2}-1)}{{1}^{2}•{2}^{2}•{3}^{2}•{4}^{2}…201{5}^{2}•201{6}^{2}}$的值应该最接近于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{2015}$ |
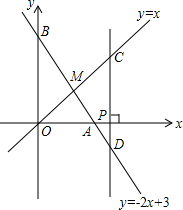 如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.
如图,已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.在X轴上有一点P(a,0)(其中a>1),过点P作x轴的垂线,分别交函数y=x和y=-2x+3的图象于点C、D.若CD=3,求a的值.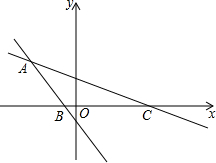 一次函数y=-x+b与y=kx+2相交于点A(-6,5),分别于x轴交于点B、C.
一次函数y=-x+b与y=kx+2相交于点A(-6,5),分别于x轴交于点B、C.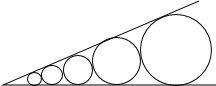 如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切,且半径分别为r1、r2、r3、r4、r5.若最小的半径r1=1,最大的半径r5=81.则sinθ=$\frac{\sqrt{3}}{2}$.
如图,在锐角θ内,有五个相邻外切的不等圆,它们都与θ角的边相切,且半径分别为r1、r2、r3、r4、r5.若最小的半径r1=1,最大的半径r5=81.则sinθ=$\frac{\sqrt{3}}{2}$. 已知一次函数y=kx+b,在x=0时的值为4,在x=-1时的值为-2,
已知一次函数y=kx+b,在x=0时的值为4,在x=-1时的值为-2,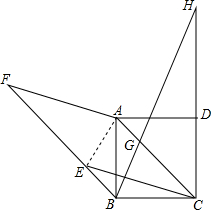 正方形ABCD,以AC为边作平行四边形ACEF,且∠ECB=15°,FE的延长线交AB于B,在AC上截取CG=BC,连接BG并延长交CD的延长线于点H.
正方形ABCD,以AC为边作平行四边形ACEF,且∠ECB=15°,FE的延长线交AB于B,在AC上截取CG=BC,连接BG并延长交CD的延长线于点H. 在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的人数是720.
在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的人数是720.