题目内容
3.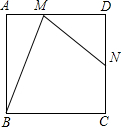 如图,在正方形ABCD中,M是AD上异于D的点,N是CD的中点,且∠AMB=∠NMB,则AM=2,求AB的长.
如图,在正方形ABCD中,M是AD上异于D的点,N是CD的中点,且∠AMB=∠NMB,则AM=2,求AB的长.
分析 根据∠NMB=∠MBC,延长MN,BC相交于T,得到等腰△TBM,连接点T和MB的中点,得到相似三角形,然后由相似三角形的性质进行计算,求出∠ABM的正切,进一步求得答案即可.
解答 解:如图: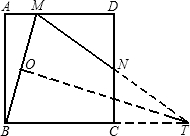
延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
∵∠ABM+∠MBT=90°,
∠OTB+∠MBT=90°,
∴∠ABM=∠OTB,则△BAM∽△TOB,
∴$\frac{AM}{OB}$=$\frac{MB}{BT}$,即$\frac{AM}{MB}$=$\frac{OB}{BT}$,即MB2=2AM•BT ①
令DN=1,CT=MD=K,则:AM=2-K,BM=$\sqrt{4+(2-K)^{2}}$,BT=2+K,
代入①中得:4+(2-K)2=2(2-K)(2+K),
解方程得:K1=0(舍去),K2=$\frac{4}{3}$.
∴AM=2-$\frac{4}{3}$=$\frac{2}{3}$.
tan∠ABM=$\frac{AM}{AB}$=$\frac{1}{3}$,
∵AM=2,
∴AB=6.
点评 本题考查了正方形的性质,勾股定理的应用,作出辅助线构建等腰三角形是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.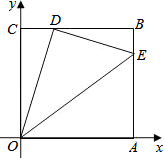 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.在实数中2,0,-4,1,-2,最大的实数是( )
| A. | -4 | B. | -2 | C. | 2 | D. | 0 |
8.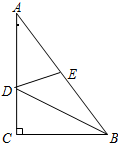 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )| A. | $\frac{\sqrt{10}}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{3}{2}$ |
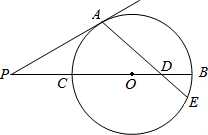 已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长.
已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长. 下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.
下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.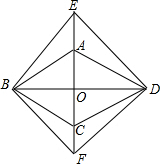 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.