题目内容
15. 如图,已知∠1=∠2,添加条件∠B=∠D后,使△ABC∽△ADE.
如图,已知∠1=∠2,添加条件∠B=∠D后,使△ABC∽△ADE.
分析 先证出∠BAC=∠DAE,再由∠B=∠D,即可得出ABC∽△ADE.
解答 解:添加条件∠B=∠D后,△ABC∽△ADE.理由如下:
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠BAC=∠DAE,
又∵∠B=∠D,
∴ABC∽△ADE.
故答案为∠B=∠D.
点评 本题考查了相似三角形的判定方法;熟练掌握三角形相似的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
5.数轴上的点A到表示-1的点B距离是6,则点A表示的数为( )
| A. | 6或-6 | B. | 5 | C. | -7 | D. | 5或-7 |
7.观察以下数组:(2),(4、6),(8、10、12),(14、16、18、20),…,问2016在第几组( )
| A. | 44 | B. | 45 | C. | 46 | D. | 无法确定 |
4.如果二次函数y=ax2+bx,当x=1时,y=2;当x=-1时,y=4,则a,b的值是( )
| A. | a=3,b=-1 | B. | a=3,b=1 | C. | a=-3,b=1 | D. | a=-3,b=-1 |

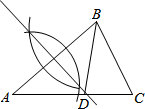 如图,在△ACB中AB=AC=6,BC=4.5,分别以点A、B为圆心,4为半径画圆弧,交于两点,过这两点的直线交AC于点D,连接BD,则△BCD的周长为( )
如图,在△ACB中AB=AC=6,BC=4.5,分别以点A、B为圆心,4为半径画圆弧,交于两点,过这两点的直线交AC于点D,连接BD,则△BCD的周长为( ) 如图,△ABC内接于⊙O,且AB=AC,AD⊥AB交⊙0于点D,AD交BC于点E,F在DA的延长线上,且AF=AE.
如图,△ABC内接于⊙O,且AB=AC,AD⊥AB交⊙0于点D,AD交BC于点E,F在DA的延长线上,且AF=AE.