题目内容
10.若关于x的二次函数y=ax2+2x-5的图象与x轴有两个交点,且有一个交点的横坐标在0和1之间(不含0和1),则a的取值范围是a>3.分析 由“关于x的二次函数y=a2+2x-5的图象与x轴有两个交点”得到△>0,然后根据有一个交点的横坐标在0和1之间(不含0和1)列出关于a的不等式并解答.
解答 解:∵关于x的二次函数y=ax2+2x-5的图象与x轴有两个交点,
∴△=4+20a>0,
解得a>-$\frac{1}{5}$.①
又∵有一个交点的横坐标在0和1之间(不含0和1),
∴当x=0时,y<0.
当x=1时,y>0,
即a-3>0,
解得a>3.②
结合①②得到:a>3.
故答案是:a>3.
点评 本题考查了抛物线与x轴的交点.解答该题时,需要掌握二次函数图象的性质.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18.近似数0.10和3.25×10-5的有效数字分别是a和b,那么ab•ba的值是( )
| A. | 3 | B. | 72 | C. | 16 | D. | 无法计算 |
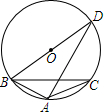 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,且BD=2,则BC=$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,且BD=2,则BC=$\sqrt{3}$. 如图,已知∠1=∠2,添加条件∠B=∠D后,使△ABC∽△ADE.
如图,已知∠1=∠2,添加条件∠B=∠D后,使△ABC∽△ADE.