题目内容
如图所示，在平行四边形ABCD中，AC与BD相交于O，E为OD的中点，连接AE并延长交CD于点F，则DF：FC等于考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：先证明△DEF∽△BEA，得出
=
，即可得出结论．
| DF |
| AB |
| 1 |
| 3 |
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，OD=OB，
∴△DEF∽△BEA，
∴
=
，
∵E为OD的中点，
∴BE=3DE，
∴
=
，
∴AB=3DF，
∴DF：CD=1：3，
∴DF：FC=1：2．
故答案为：1：2．
∴AB∥CD，AB=CD，OD=OB，
∴△DEF∽△BEA，
∴
| DF |
| BA |
| DE |
| BE |
∵E为OD的中点，
∴BE=3DE，
∴
| DF |
| BA |
| 1 |
| 3 |
∴AB=3DF，
∴DF：CD=1：3，
∴DF：FC=1：2．
故答案为：1：2．
点评：本题考查了平行四边形的性质和相似三角形的判定与性质；熟练掌握相似三角形的性质是关键．
练习册系列答案
阅读快车系列答案
相关题目
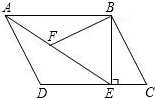如图，在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠AFB=∠D．
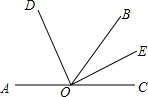如图所示，∠AOB与∠BOC互为补角，OD平分∠AOB，OE平分∠BOC，求∠DOE的度数．
有一个可以自由转动的转盘，被分成了4个相同的扇形，分别标有数1、2、3、4（如图所示），另有一个不透明的口袋装有分别标有数0、1、2的三个小球（除数字不同外，其余都相同）．小亮转动一次转盘，停止后指针指向某一扇形，记下扇形所对应的数，
如图，等腰三角形ABC中，AB=AC，点D在BC边上，连接AD，点E在直线抽样调查了某校30为女生所穿鞋子的尺码，数据如下（单位：码）．在这组数据的平均数、中位数和众数中，鞋厂最感兴趣的是（ ）
| 码号 | 33 | 34 | 35 | 36 | 37 |
| 人数 | 7 | 6 | 15 | 1 | 1 |
| A、平均数 | B、中位数 |
| C、众数 | D、无法确定 |
