题目内容
7. 如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )
如图,已知AC与BC相交于点O,∠C=∠D=75°,∠A=35°,则∠B的度数为( )| A. | 25° | B. | 35° | C. | 40° | D. | 45° |
分析 根据三角形的内角和定理求出∠AOD,根据对顶角相等可得∠BOC=∠AOD,再根据三角形的内角和等于180°列式计算即可得解.
解答 解:在△AOD中,∵∠D=75°,∠A=35°,
∴∠AOD=180°-∠A-∠D=180°-35°-75°=70°,
∵∠BOC=∠AOD=70°(对顶角相等),
∴在△BOC中,∠B=180°-∠BOC-∠C=180°-70°-75°=35°.
故选B.
点评 本题考查了三角形的内角和定理,对顶角相等的性质,熟记定理并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.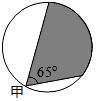 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )| A. | 25° | B. | 65° | C. | 115° | D. | 130° |
 如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F.
如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F. 如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.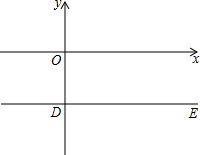 已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.
已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A. 已知:如图,四边形ABCD中,∠A=∠C=90°,∠D=60°,AD=5$\sqrt{3}$,AB=3,求BC的长.
已知:如图,四边形ABCD中,∠A=∠C=90°,∠D=60°,AD=5$\sqrt{3}$,AB=3,求BC的长.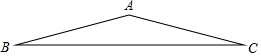 如图,三角形ABC中,AB=AC=2,∠B=15°,求AB边上的高.
如图,三角形ABC中,AB=AC=2,∠B=15°,求AB边上的高.