题目内容
19．
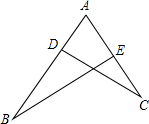如图，点D在AB上，点E在AC上，且AD=$\frac{1}{3}$AC，AE=$\frac{1}{3}$AB．求证：△ABE∽△ACD．
分析 利用AD=$\frac{1}{3}$AC，AE=$\frac{1}{3}$AB易得$\frac{AD}{AC}$=$\frac{AE}{AB}$，则利用比例性质得$\frac{AD}{AE}$=$\frac{AC}{AB}$，加上∠DAC=∠EAB，于是根据两组对应边的比相等且夹角对应相等的两个三角形相似即可得到结论．
解答 证明：∵AD=$\frac{1}{3}$AC，AE=$\frac{1}{3}$AB，
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$，
∴$\frac{AD}{AE}$=$\frac{AC}{AB}$
∵∠DAC=∠EAB，
∴△ABE∽△ACD．
点评 本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
9．点P（2，3）关于原点的对称点的坐标是（ ）
| A． | （2，3 ） | B． | （-2，-3） | C． | （-2，3） | D． | （-3，2） |
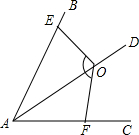如图，∠BAC=60°，O是∠BAC平分线上的一点，点E、F分别在AB、AC上，若∠EOF=120°，求证：OE=OF．